Дана система m линейных уравнений с n неизвестными
;
Решением этой системы называется совокупность п чисел (х1, х2, …, хn), которые, будучи подставлены вместо неизвестных в уравнения, обращают эти уравнения в тождества. Система уравнении называется совместной, если она имеет хотя бы одно решение (х1, х2, …, хn). Если же система не имеет ни одного решения, то она называется несовместной.
Совместная система называется определенной, если она имеет только одно решение, и неопределенной, если она имеет больше одного решения.
Матрица А составленнаяиз коэффициентов при неизвестных называются матрицей системы, а матрица А1 , составленная из коэффициентов при неизвестных и столбца свободных членов, называется расширенной матрицей этой системы.
; А1 = 
Теорема Кронекера—Капелли: Для совместности системы необходимо и достаточно, чтобы ранг матрицы этой системы А равнялся рангу ее расширенной матрицы А1.
Итак, система совместна тогда и только тогда, когда D (A) = D (A1).= r. В этом случае число r называется рангом системы.
Если же ранг совместной системы меньше числа неизвестных, то система — неопределенная. Остановимся на последнем случае. Итак, предположим, что система совместна, причем r<п. Рассмотрим какой-нибудь базисный минор матрицы А. Выделим в этом миноре произвольную строку. Элементы этой строки являются коэффициентами при r неизвестных в одном из уравнений системы. Эти r неизвестных назовем базисными неизвестными рассматриваемой системы уравнений. Остальные п—r неизвестных системы назовем свободными неизвестными.
Выделим из системы уравнений систему r уравнений, среди коэффициентов которых содержатся элементы базисного минора. Базисные неизвестные в выделенной системе оставим в левых частях уравнений, а члены, содержащие свободные неизвестные, перенесем вправо. Из полученной системы уравнений выразим базисные неизвестные через свободные неизвестные (например, по формулам Крамера).
Таким образом, придавая свободным неизвестным произвольные значения можно найти соответствующие значения базисных неизвестных. Следовательно, система имеет бесчисленное множество решений.
Пример. Исследовать систему уравнений:
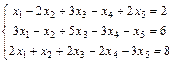
Решение: Вычислим ранг матрицы А и ранг расширенной матрицы A1
А =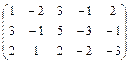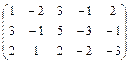 
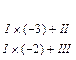r 
~r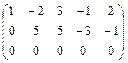 
~
r 
~r 
D (A)=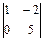 
= 1´5 - 0´(-2) = 5¹0, значит ранг матрицы А равен 2.
A1= 
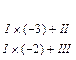r ~r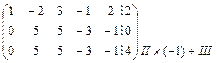 
~
r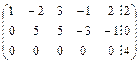 
D (A1)= 
= (-1)´1´4 + (-3)´0´2 + 2´0´0 - 2´1´0 - (-3)´2´4 -0´0´2=20¹0, значит расширенной ранг расширенной матрицы A1 равен3.
Значит, система несовместна, решений нет.
Пример. Исследовать систему уравнений.
Решение:
Ранг матрицы А и расширенной матрицы А1 равны 3, значит система совместна. Определитель 3-го порядка
D3 = 
= -10 + (-2) + 3 – (-12) – 1 - (-5) = 27 ¹ 0
Так как ранг матрицы равен числу неизвестных, то значит, система совместна. Решим систему первых трех уравнений.
, решая систему, например, методом Крамера, получаем
х1 =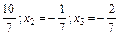 
, это же решение удовлетворяет и четвертому уравнению.
Пример. Исследовать систему уравнений
Решение:
Вычислим ранг матрицы А и ранг расширенной матрицы A1.
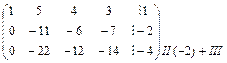r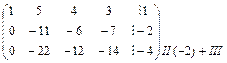 
~r 
~
r ~r 
~r 
D (A)= D (A1) = 
= -11 ¹ 0, ранг матрицы и ранг расширенной матрицы равны, значит система совместна и неопределенная.
Возьмем 1 и 2 уравнения системы. За базисные возьмем х1 и х2,так как определитель из коэффициентов при этих неизвестных отличен от нуля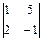 
= -1 –10 = -11 ¹ 0.
Свободными будут х3 и х4.
.
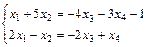Выразим х1 и х2 через х3 и х4. По формуле Крамера:
;
Полагая х3 = u, x4 = v, получаем: 
, 
. Придавая u и v различные значения, будем получать различные решения этой системы. Частное решение найдем, придавая u и v какие либо числа. Например, х3 = 11, x4 = -22 => х1 = 
, х2 = 
.
