Два режима движения вязкой жидкости

 

В 1880 г. Д.И. Менделеев в работе «О сопротивлении жидкости и воздухоплавании» впервые высказал предположение о существовании двух, совершенно различных по структуре потока режимов движения жидкости. Спустя три года английский учёный Осборн Рейнольдс открыл оба эти режима экспериментальным путём.

Выяснилось, что при малых скоростях течения частицы движутся только вдоль оси потока параллельными траекториями, то есть поток как бы состоит из отдельных слоёв. Такой режим движения получил название ламинарного. При более высоких скоростях течения наряду с основным поступательным движением по некоему среднему направлению наблюдаются незакономерные поперечные и вращательные перемещения отдельных объёмов жидкости.

Этот режим движения жидкости получил название турбулентного. Визуально, указанные режимы течения жидкости можно наблюдать на приборе Рейнольдса.

1 – бак с исследуемой жидкостью; 2 – трубка; 3 – кран; 4 – измерительный сосуд; 5 – бак с однотипной жидкостью другого цвета.

Жидкость в баке 5 подкрашивается лёгким красителем, чтобы не было различия в удельном весе, вязкости и других свойствах.

Рис.3.10

При малых скоростях движения подкрашенная жидкость будет перемещаться в виде отдельной струйки. Если к трубке 2 подвести несколько наконечников, то подкрашенная жидкость будет перемещаться несколькими параллельными подкрашенными струйками. При дальнейшем увеличении средней скорости потока до определённой критической скорости будет так же наблюдаться ламинарный режим движения жидкости. Далее ламинарный режим нарушается и сменяется турбулентным режимом движения (струйка колеблется, затем активнее перемешивается). При дальнейшем увеличении скорости течения интенсивность перемешивания увеличивается.

Если же опыт произвести в обратном порядке, то есть идти от больших скоростей к меньшим, то турбулентный режим в определённое время сменится ламинарным. Однако этот переход произойдёт при заметно меньшем значении критической скорости, чем переход от ламинарного режима к турбулентному.

Таким образом, здесь отмечаются две критические скорости:

V_вк - верхняя критическая (переход ламинарного режима в турбулентный);

V_нк - нижняя критическая (переход турбулентного режима в ламинарный).

В диапазоне от V_вк к V_нк возможен и тот, и другой режимы, однако ламинарный режим движения в этой зоне очень неустойчив. Достаточно малейшего возмущения потока, чтобы произошёл преждевременный срыв ламинарного режима с последующим переходом в турбулентный. С другой стороны, при очень тщательно поставленных опытах иногда удаётся сохранить ламинарный режим при скорости, превышающей обычные значения V_вк. В результате исследований установлено, что режим движения зависит от средней скорости потока V, динамического коэффициента вязкости жидкости μ, её плотности ρ и поперечного размера потока.

Для характеристики режима движения жидкости в круглой трубе Рейнольдс предложил безразмерный параметр, который в последствии получил его имя – число Рейнольдса.

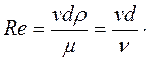(3.62)

Многочисленными опытными исследованиями так же установлено, что нижней критической скорости для всех жидкостей соответствует число Рейнольдса

Rе _кр = 2320 (для труб);

Rе _кр = 580 (для открытых русел).

Поэтому для аналитического определения режима движения потока достаточно подсчитать Rе _кр. Если Rе > Rе _кр, то режим движения – турбулентный; если Rе < Rе _кр – ламинарный.

Важнейшим результатом открытия ламинарного и турбулентного режимов движения жидкости явилось установление положения о том, что характер движения оказывает существенное влияние на формирование потерь напора. Установлено, что удельная сила трения τ₀ и потери напора h_w при ламинарном режиме пропорциональны средней скорости в первой степени, а при турбулентном – в степени n. При этом показатель n в области устойчивых турбулентных режимов равен 2, следовательно

τ₀ = bV², (3.63)

h_w = BV², (3.64)

где b и B – коэффициенты пропорциональности.

В области турбулентного режима, близко прилегающего к ламинарному, 1< n <2.

 

3.10.1 Ламинарный режим движения жидкости в трубах

Жидкость, движущуюся по трубе в ламинарном режиме, можно представить состоящей из концентрических слоёв, перемещающихся относительно друг друга вдоль трубы. Первый слой, состоящий из частиц жидкости, прилипших к стенкам трубы, не участвует в движении. Для этого слоя скорость u = 0. Второй концентрический слой с небольшой скоростью перемещается вдоль трубы и скользит по первому слою. Третий слой, обладая более высокой скоростью, скользит по второму слою и т. д. Очевидно, что последний слой жидкости, находящийся на оси трубы, будет перемещаться с наибольшей скоростью.

Вследствие относительного перемещения, между каждой парой соседних слоёв возникают силы трения – силы гидравлического сопротивления, препятствующие движению жидкости.

Рис.3.11

Применим основное уравнение равномерного движения к движущемуся цилиндру жидкости с произвольным радиусом h и длиной l

, (3.65)

где τ – касательное напряжение.

Гидравлический радиус в данном случае

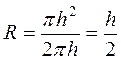. (3.66)

Решая уравнение (3.65), относительно τ, и подставив в него уравнение (3.66), получим

 

. (3.67)

Следовательно, касательные напряжения в какой-либо точке поперечного сечения пропорциональны её расстоянию от оси трубы. На оси трубы, где h = 0 и τ = 0. Участок трубы, где h = r, касательные напряжения принимают максимальное значение и равны τ₀ (рис.3.11).

Выразим в уравнении (3.67) касательные напряжения τ в соответствии с законом Ньютона

. (3.68)

Знак «–» указывает, что положительному приращению радиуса соответствует отрицательное приращение скорости (рис.3.11).

Решим уравнение (3.68) относительно du и проинтегрируем

. (3.69)

Постоянную интегрированияполучим из условий движения жидкости у стенки трубы при h = r, u = 0

С = . (3.70)

Тогда, уравнение (3.69) примет вид

. (3.71)

Следовательно, при ламинарном режиме движения жидкости, скорости в различных точках поперечного сечения потока изменяются по закону параболы. У стенок трубы, при h = r: u = 0; на оси потока, при h = 0: u = max, т.е. скорость достигает максимального значения и равна

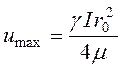(3.72)

Среднюю скорость движения жидкости найдём как частное от деления полного расхода потока Q на площадь поперечного сечения потока (конечная формула)

, (3.73)

то есть средняя скорость оказалась равна половине максимальной скорости.

Определим потерю напора h_w при движении жидкости в пределах рассматриваемого участка трубы. Для этого в уравнении (3.73) заменим гидростатический уклон I на и решим это уравнение относительно h_w

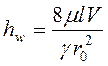. (3.74)

Из формулы (3.74) видно, что потери напора при ламинарном режиме движения жидкости прямо пропорциональны средней скорости потока.

Формулу (3.74) в результате преобразований можно привести к универсальному виду

(3.75)

Обозначив λ = 64 /Rе, окончательно получим известную в гидравлике формулу Дарси

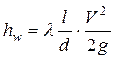(3.76)

где λ – коэффициент сопротивления трения, зависящий при ламинарном режиме только от числа Рейнольдса и совершенно не зависящий от шероховатости стенок трубы.

Необходимо отметить, что величина λ для ламинарного потока весьма чётко реагирует на искажения живого сечения цилиндрической трубы (сплющивание, вмятины и т. д.)

Опыт эксплуатации реальных жёстких трубопроводов показывает, что в них

, (3.77)

а в резиновых шлангах

. (3.78)

 

3.10.2 Турбулентный режим движения жидкости

 

При турбулентном режиме структура потока жидкости несколько иная, чем при ламинарном. Турбулентность является одним из сложнейших гидравлических явлений. При турбулентном движении скорости отдельных частиц жидкости, в отдельных точках пространства занятого жидкостью всё время меняются по величине и направлению. Это изменение скоростей в данной точке пространства, занятого жидкостью, называется пульсацией скоростей.

Несмотря на кажущуюся беспорядочность изменения скоростей при турбулентном режиме, оказывается, что мгновенные скорости u в данной точке пространства колеблются около некоторой постоянной величины, называемой осреднённой скоростью u_ср.

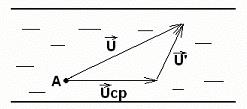Мгновенное значение вектора скорости в точке можно представить как сумму осреднённой скорости и переменной по направлению и во времени пульсационной составляющей u’

 

Рис.3.12 . (3.79)

 

Из рис.3.12 видно, что осреднённая скорость направлена вдоль оси потока. Пульсационная составляющая может иметь любое направление. В пропорциях на координатные оси она равна

. (3.80)

Если с помощью специального датчика записать величину пульсационной составляющей по какому-либо направлению, то зависимость пульсации скорости от времени будет иметь вид, характерный для случайных процессов. Средняя величина пульсаций за достаточно большой промежуток времени равна нулю.

Рис.3.13

 

Исследованиями установлены три характерные области поперечного сечения турбулентного потока.

Рис.3.14

Непосредственно у поверхности трубы находится весьма тонкий слой, называемый ламинарной плёнкой, где движение жидкости происходит в ламинарном режиме. Его толщина δ_пл измеряется в долях мм. Второй, также сравнительно тонкий слой является переходной зоной от ламинарного к турбулентному движению жидкости. Ламинарная плёнка и переходный подслой составляют вместе пограничный слой, непосредственно граничащий со стенками трубы или какого-либо русла. Всю остальную площадь поперечного сечения трубы занимает ядро потока, движущееся в турбулентном режиме.

Для выяснения закономерностей изменения скоростей и сил трения по сечению потока при турбулентном режиме, рассмотрим понятие о шероховатости стенок, ограждающих поток.

Шероховатость является одной из причин появление дополнительных гидравлических сопротивлений и потерь энергии при движении потока. Для оценки выступов шероховатости в гидравлике введено понятие абсолютной шероховатости Δ.

а) б)

Рис.3.15

Если ламинарный подслой покрывает выступы шероховатости, то труба считается гидравлически гладкой (рис.3.15а), и наоборот, если выступы шероховатости больше, чем толщина ламинарного подслоя, труба называется гидравлически шероховатой (рис.3.15б).

Отношение абсолютной шероховатости Δ к радиусу трубы r называется относительной шероховатостью ε

ε . (3.81)

3.10.3 Силы трения и закон распределения скоростей

при турбулентном режиме

 

За счёт активного перемещения жидкость при турбулентном режиме её движения появляются дополнительные потери энергии и возникают дополнительные касательные напряжения (это связано с беспорядочным движением частиц).

При рассмотрении ламинарного режима движения жидкости касательные напряжения мы определяли, используя закон трения Ньютона.

При турбулентном движении ввиду отсутствия слоистости потока этот закон не применим. Здесь мы используем следующее уравнение

, (3.82)

где l – условный коэффициент, имеющий линейную размерность и названный Прандтлем «длиной пути перемешивания». По гипотезе Прандтля величина l прямо пропорциональна удалению от стенок канала

, (3.83)
где = r – h (рис.3.14); k – коэффициент пропорциональности, называемый универсальной постоянной. По данным Г.А. Гуржиенко k = 0.4. Следовательно, l =0.435 y.

Первый член уравнения (3.81) 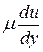характеризует вязкое трение, которое соответствует силе трения в ламинарном режиме. Второй член этого уравнения выражает дополнительные касательные напряжения от пульсаций и с увеличением числа Рейнольдса оказывает наибольшее влияние на величину касательных напряжений.

Для развитого турбулентного режима (то есть при больших значениях Re) первый член уравнения по сравнению со вторым является очень малой величиной. Это связано с тем, что в пограничном слое участвует очень малая масса жидкости то есть толщина пограничного слоя очень сильно уменьшается. Поэтому им можно пренебречь.

Тогда уравнение (3.81) будет иметь вид

, (3.84)

или . (3.85)

Комплекс 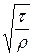имеет размерность скорости, и получил название «динамическая скорость» u_д.

. (3.86)

 

Подставим (3.82) и (3.85) в уравнение (3.84) и перепишем его относительно du_ср

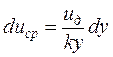. (3.87)

 

Примем u_д = const, тогда после интегрирования

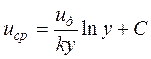. (3.88)

Постоянная интегрирования С находится из условия, что на оси потока при h =0, u_cp = u. С учётом этого осреднённые значения скорости на расстоянии h от оси потока будут равны

. (3.89)