Полные потери напора в каком-либо трубопроводе слагаются из потерь напора на трение и потерь напора, вызванных местными сопротивлениями. Подобное геометрическое суммирование потерь напора по всему пути движения жидкости в трубопроводе носит название принципа наложения потерь. Если в трубопроводе, состоящем из нескольких участков последовательно соединённых труб, имеются различные местные препятствия, то суммарная потеря напора равна
. (3.106)
Рассмотрим несложную систему трубопровода, представленную на рис.3.18.
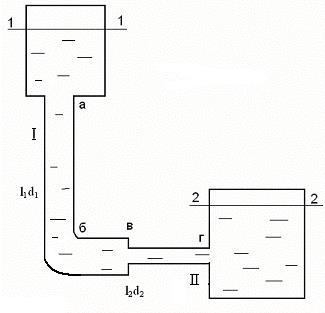Трубопровод состоит из 2х участков труб, все размеры которых и гидравлические характеристики известны. В данной системе возникнут потери:
1. на трение на участках I и II;
2. на входе в трубу (а);
3. в повороте (б);
Рис.3.18 4. во внезапном сужении (в);
5. на выходе из трубы (г).
Тогда полные потери напора составятся из суммы:
. (3.107)
Сгруппировав слагаемые с общими множителями, получим
. (3.108)
По условию неразрывности потока имеем
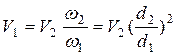. (3.109)
Подставим (3.109) в (3.108)
. (3.110)
Выражение, стоящее в квадратных скобках, представляет собой коэффициент сопротивлений данной системы трубопроводов ξсист. В результате, выражение суммарных потерь напора приобретает краткую запись в виде формулы Вейсбаха
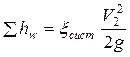. (3.111)
Таким образом, коэффициентом сопротивления системы называется сумма всех коэффициентов сопротивлений, приведённых к единому скоростному напору.
Запишем уравнение Бернулли для жидкости, перетекающей из левого бака в правый. В качестве характерных сечений возьмем свободные поверхности 1-1 и 2-2, за плоскость сравнения примем плоскость 2-2. Скоростными напорами в сечениях пренебрегаем.
. (3.112)
Давления на свободной поверхности одинаковы и равны атмосферному, поэтому
. (3.113)
Координата z1 – это исходный геометрический напор жидкости Н, находящейся в левом баке. Координата z2 характеризует запас удельной энергии положения после перемещения жидкости через сопротивления из левого бака в правый. Назовём эту величину свободным напором после сопротивления 
, следовательно
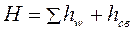, (3.114)
то есть располагаемый напор истрачен на преодоление сопротивлений и создание свободного напора.
Выразим скорость V2 через расход 
и подставим в уравнение (3.111)
. (3.115)
Коэффициент Ксист связывает суммарные гидравлические потери в системе с протекающим расходом. Подставим (3.114) в (3.113) и окончательно получим
. (3.116)
Это уравнение называется характеристикой системы и показывает, каким напором необходимо располагать, чтобы обеспечить в системе заданный расход Q и свободный напор на выходе hсв .
