Величина коэффициента гидравлического трения λ зависит от числа Рейнольдса и относительной шероховатости стенок, то есть λ = f(Re, Δ /r).
Впервые исследования по установлению этой закономерности были выполнены в 1932 г. Никурадзе и в 1938 г. профессором А.П. Зегжда (СССР).
Никурадзе были построены кривые по результатам экспериментальных исследований для труб с искусственной шероховатостью. Из полученных им графиков следует, что при движении жидкости в напорном трубопроводе можно выделить 3 области.
I область относится к ламинарному режиму движения жидкости. Эта область ограничена значениями чисел Re < 2320. Здесь λ зависит только от Re и не зависит от шероховатости
. (3.90)
Потери напора в этой области пропорциональны скорости течения жидкости в первой степени.
II область– турбулентный режим движения жидкостив гидравлически гладких трубах, когда выступы шероховатости меньше толщины ламинарного слоя. Коэффициент λ можно определить по формуле Блазиуса (1913 г.)
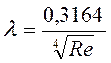для 2320 < Re <100 000 (3.91)
или по формуле П.К. Конакова (1946 г.)
. (3.92)
III область является областьюквадратичных сопротивлений, которая наступает при Re >1120 r/Δ.. Данные по абсолютной величине шероховатости Δ имеются в справочной литературе.
Без существенных ошибок величину λ в этой области можно определить по упрощенной универсальной формуле А.Д. Альтшуля
(3.93)
где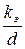 
– абсолютная величина эквивалентной равномерно-зернистой шероховатости. Значения 
имеются в справочных изданиях.
Эта область соответствует турбулентному режиму движения жидкости, когда потери напора пропорциональны квадрату скорости течения жидкости.
Гидравлические потери
Потери удельной энергии (напора) или гидравлические потери зависят от формы, размеров и шероховатости русла (трубы и т.п.), а так же от скорости течения и вязкости жидкости, но практически не зависят от абсолютного значения давления в ней.
В большинстве случаев гидравлические потери примерно прямо пропорциональны квадрату скорости течения жидкости, поэтому в гидравлике принято выражать гидравлические потери полного напора в линейных единицах.
, (3.94)
где коэффициент 
– есть безразмерный коэффициент сопротивления, выражающий отношение потерянного напора к скоростному напору.
Гидравлические потери разделяют на местные и потери на трение.
Местные потери обусловлены так называемыми местными гидравлическими сопротивлениями (изменение формы и размеров русла, в трубах – повороты, диафрагмы, краны и т.п.).
Потери на трение или потери по длине – это потери энергии, которые возникают в прямых трубах постоянного сечения. Они обусловлены внутренним трением в жидкости, а потому имеют место не только в шероховатых, но и в гладких трубах.
Коэффициент сопротивления на трение в этом случае удобнее связать с относительной длиной трубы
, (3.95)
где 
- безразмерный коэффициент потерь на трение.
3.12.1 Местные потери напора
Местные потери напора возникают на относительно коротких участках потока, где происходит изменение величины и направления средней скорости. Подобные изменения скорости обычно имеют место в фасонных частях и арматуре трубопроводов – в отводах, переходах, тройниках, кранах, вентиляциях, клапанах и т. п. Движение жидкости в области местных препятствий сопровождается резким нарушением структуры потока, образования дополнительных вихрей и водоворотных зон, закручиваний и нарушений стройности потока.
Несмотря на многообразие геометрических конфигураций местных сопротивлений, в каждом из них можно выделить участок, где поток вынужден резко уменьшать или увеличивать свою среднюю скорость. Иногда местное сопротивление представляет последовательное чередование таких участков.
Поэтому изучение местных сопротивлений целесообразно начать с простейшего случая – внезапного расширения потока (рис.3.16).
Рис. 3.16
Местная потеря напора, вызванная внезапным расширением потока на участке между сечениями 1-1 и 2-2, определится как разность удельных энергий жидкости в сечениях:
. (3.96)
Для определения разности давлений, входящей в уравнение (3.95) применим к движущему объёму жидкости между сечениями 1-1 и 2-2 известную из механики теорему об изменении количества движенияв проекциях на ось потока S-S.
Для этого:
1) определим импульс внешних сил, действующих на рассматриваемый объём в направлении движения;
2) найдём изменение количества движения как разность между секундным количеством движения, выносимым из рассматриваемого объёма и вносимым в него.
После преобразований получим:
. (3.97) Из формулы (3.97) видно, что потеря напора (удельной энергии) при внезапном расширении русла равна скоростному напору, подсчитанному по разности скоростей. Это положение называется теоремой Борда-Карно.
Потери напора при внезапном расширении можно отнести либо к V1, либо к V2. Если учесть, что V1ω1 = V2ω2 то есть V2 = V1ω1 /ω2 (согласно уравнения неразрывности), то формулу (3.97) можно записать в следующем виде, соответствующем общему способу выражений местных потерь
. (3.98)
Уравнение (3.98) называют формулой Вейсбаха.
Следовательно, для случая внезапного расширения русла коэффициент сопротивления равен
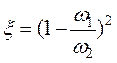. (3.99)
Данная теорема хорошо подтверждается опытными данными при турбулентном течении и широко используется в расчётах.
В частном случае, когда площадь ω2 весьма велика по сравнению с площадью ω1 и, следовательно, скорость V2 можно считать равной нулю, потеря на расширение равна
, (3.100)
то есть в этом случае теряется весь скоростной напор (вся кинетическая энергия, которой обладает жидкость). Коэффициент сопротивления ξ в этом случае равен единице.
Рассмотрим случай внезапного сужения канала.
Рис.3.17
При внезапном сужении, как показывают многочисленные опыты, поток жидкости начинает сжиматься на некотором расстоянии перед входом в узкое сечение. После входа в узкий участок, вследствие инерции, сжатие потока продолжается до минимального сечения ωс, после чего струя начинает расширяться до тех пор, пока не заполнит всё сечение узкого участка трубопровода ω2. потери напора при взаимном движении hв .с. при переходе потока из сечения ω1 к сечению ω2 связаны с расширением струи на участке С-С – 2-2 и могут быть найдены по формуле Борда
, (3.101)
а с учётом уравнения неразрывности
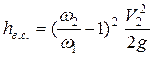. (3.102)
Отношение площади сжатого сечения струи к площади канала, где это сжатие наблюдается, называется коэффициентом сжатия струи
; (3.103)
С учётом этого
. (3.104)
Опыт показывает, что величина ε зависит от соотношения площадей трубопровода до и после сужения.
. (3.105)
Мы рассмотрели два вида местных потерь напора – при внезапном расширении и сужении трубопровода, в которых коэффициент сопротивления определяется теоретически. Для всех остальных местных сопротивлений величину коэффициента сопротивления определяют опытным путём.
Наиболее часто встречающиеся местные сопротивления:
- труба расположена под углом к стенке резервуара;
- труба расположена перпендикулярно стенке резервуара;
- колено трубы с закруглением на угол 900;
- резкий поворот трубы и т. п.
Численные значения коэффициентов сопротивления для этих случаев обычно приводятся в справочной литературе.
В заключении следует отметить, что величина местного сопротивления остаётся постоянным лишь при развитом турбулентном режиме при Re >3000. В переходной зоне и при ламинарном режиме (Re < 3000) следует учитывать увеличение ξ, вызываемое существенным влиянием сил вязкостного трения.
