По конструкции и гидравлическим условиям работы трубопроводы делятся на простые и сложные, гидравлически длинные и короткие.
Простым называется трубопровод, состоящий из последовательно соединённых труб одного или нескольких диаметров, без ответвлений, но по всей длине которого протекает постоянный расход. Все остальные трубопроводы относятся к сложным, например, разветвлённые параллельно кольцевые и трубопроводы с переменным расходом жидкости по длине.
Длинными считаются такие трубопроводы, в которых на всём протяжении основными потерями напора являются потери напора на преодоление трения. Местные же потери напора невелики, они составляют не более 5-10% от общих потерь. Поэтому при расчёте длины трубопроводов местными потерями либо пренебрегают, либо с целью их приблизительного учёта производят увеличение потерь за счёт дополнительной эквивалентной длины, то есть расчетная длина трубопровода будет на 5-10% больше действительной.
l расч = (1.05…1.1) l. (3.117)
К длинным трубопроводам, в частности, относятся трубопроводы сети водоснабжения, нефтепроводы, газопроводы и другие трубопроводы, имеющие значительную протяженность.
В коротких трубопроводах местные потери напора составляют существенную долю суммарных потерь – более 10%. Поэтому при расчетах коротких трубопроводов наряду с потерями на трение подлежат обязательному расчету и местные потери напора. К коротким трубопроводам относятся всасывающие трубопроводы насосов, сифонные трубопроводы, топливопроводы, маслопроводы систем гидропривода и трубопроводы гидравлических систем двигателей станков, механизмов и технологических линий.
Рассмотрим задачи гидравлического расчёта простейшего трубопровода, состоящего из труб одного диаметра (рис.3.19), где жидкость из-за разности уровней в резервуарах, равной H, перетекает из резервуара I в резервуар II с некоторым расходом Q.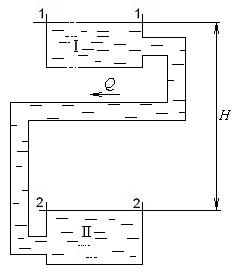 
1. Определим необходимый напор H, обеспечивающий заданный расход Q при известных размерах трубопровода l и d. Для этого составим уравнение Бернулли относительно сечений 1-1 и 2-2. Принимая, что V1 = V2 и р1 = р = р2 = ратм, получим z1 = z2 + hw,
Рис. 3.19 отсюда H = z1 – z2 = hw.
То есть, весь располагаемый напор полностью расходится на преодоление гидравлических сопротивлений в трубопроводе. Этот напор H сложится из потерь на трение (путевых потерь) и местных потерь напора
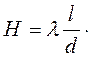
. (3.118)
2. Определим расход жидкости Q при известных диаметрах, длинах трубопровода и напоре H. В данной задаче с помощью (3.118) находим скорость
. (3.119)
Тогда исходный расход найдётся из выражения
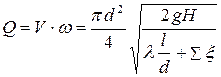. (3.120)
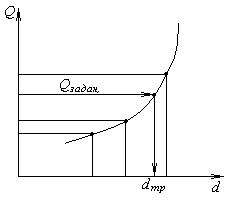3. Определим диаметр трубопровода dтр при заданном расходе жидкости, напоре и остальных параметрах. Данная задача решается методом последовательных приближений, для чего задаются произвольным значением d и по формуле (3.120) определяют расход Q. При несовпадении найденного значения расхода с заданным принимают другое значение d и расчёт повторяют. Решение задачи может быть ускорено при помощи графика (рис.3.20). На основании не менее, чем четырёх попыток расчёта строится кривая 
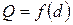. Искомый диаметр трубопровода dтр может быть найден графически. Если местные потери в трубопроводе незначительны, и ими можно пренебречь, то при наличии справочных таблиц со значениями расходных характеристик все три задачи решаются значительно быстрее.
Рис. 3.20
3.15 Гидравлический удар в трубах
Гидравлическим ударом называется резкое изменение давления в трубопроводе, вызванное внезапным изменением скорости движения жидкости в нём. Различают положительный и отрицательный гидравлический удар. Положительный удар возникает при внезапном уменьшении скорости движения жидкости. В этом случае давление в трубопроводе увеличивается.
Отрицательный удар характеризуется уменьшением давления в трубопроводе. За процессом развития явления гидроудара можно проследить на трубопроводе, схема которого представлена на рис.3.21. Из резервуара а жидкость движется по
Рис.3.21 трубопроводу в сторону
задвижки б. В результате внезапного закрытия задвижки, произойдёт резкое торможение движения жидкости, но остановка всей массы жидкости произойдёт не сразу. В первый момент остановится слой жидкости, непосредственно примыкающий к задвижке. Вся остальная масса жидкости, стремясь сохранить первоначальное направление движения, окажет давление на передний, уже остановившейся слой и т. д. вплоть до напорного резервуара а. При этом одновременно с уплотнением жидкости будет происходить увеличение давления в трубопроводе.
Таким образом, в начале удара зона повышения давления в виде волны будет распространяться по трубопроводу с некоторой скоростью с в направлении противоположном давлению жидкости.
Скорость с называется скоростью распространения ударной волны. Для большинства трубопроводов значение этой скорости весьма велики и достигают величины 1000 м/с и более. Поэтому данный процесс протекает очень быстро.
Повышение внутреннего давления в трубе вызывает в свою очередь расширение её стенок, поэтому вместе с перемещением ударной волны происходит перемещение и зоны деформации трубопровода.
При достижении у задвижки максимума давления жидкости, жидкость устремляется обратно в резервуар в виде ударной волны с той же скоростью с. Такой цикл повторяется несколько раз. В конце концов вследствие затрат энергии на сжатие жидкости и деформацию стенок трубопровода про- цесс затухает.
Изобразим диаграмму изменения давления во времени в процессе развития гидравлического удара.
Рис.3.22
Из диаграммы (рис.3.22) видно, что наиболее высокое давление в трубопроводе наблюдается не в самом начале удара, а несколько позднее. Это объясняется тем, что явление удара происходит в упругой среде.
Явление гидравлического удара было открыто и впервые экспериментально и теоретически исследовано профессором Н.Е. Жуковским в 1898 г.
Различают прямой (при быстром закрытии задвижки) и не прямой (при медленном закрытии задвижки) гидравлический удар.
При прямом ударе время закрытия задвижки, намного меньше времени возвращения ударной волны, то есть Т3 << T. Время пробега ударной волны от задвижки к напорному резервуару и обратно называется продолжительностью фазы гидравлического удара или временем цикла.
. (3.121)
Для определения величины повышения давления Δ р при прямом гидравлическом ударе профессором Жуковским впервые была выведена следующая формула
, (3.122)
где V - величина потерянной скорости.
Скорость распространения ударной волны так же определяется по формуле Жуковского:
, (3.123)
где Е0 – модуль упругость жидкости; Е – модуль упругости материала стенок труб; d – диаметр трубы; δ – толщина стенок трубы.
Числитель формулы (3.122) есть известная в физике формула Ньютона для определения скорости звука в неограниченной жидкой среде. Для воды эта скорость равна 1425 м/с
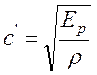. (3.124)
Отметим, что для обычных стальных и чугунных водопроводных труб общего применения скорость распространения ударной волны имеет значение около 1000 – 1300 м/с. Это значит, что каждый потерянный метр скорости движения воды, согласно формуле (3.121) вызывает повышение давления в трубопроводе на 10-13 атмосфер.
Эластичные трубопроводы, обладающие малыми модулями упругости (например, резиновые шланги) дают очень низкие значения скоростей с, а поэтому повышение давления в них при внезапном закрытии затвора невелико.
При непрямом ударе время закрытия задвижки превышает длительность фазы гидравлического удара, то есть Т3 > T. В этом случае повышение давления может быть посчитано по формуле
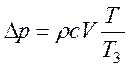. (3.125)
Гидравлический удар является весьма нежелательным явлением в эксплуатации трубопроводных систем. Прямой гидравлический удар может привести к разрушению трубопровода. Поэтому при расчете и проектировании трубопроводных систем следует предусматривать мероприятия по снижению или ликвидации гидроудара.
Основной мерой борьбы с гидроударом является увеличение времени закрытия задвижки (затворы вентильного типа).
При внезапной остановке насосов, турбин и т.п. на трубопроводах устанавливается специальная арматура в виде предохранительных клапанов, клапанов-гасителей и иных устройств, снижающих эффект гидравлического удара.
Гидропривод
