В расчётной практике важно уметь определять давление жидкости на криволинейные поверхности.
Определение силы гидростатического давления на криволинейные поверхности усложняется тем обстоятельством, что элементарные силы dF, приложенные к элементам площади 
, имеют различные направления. Поэтому отыскание равнодействующей гидростатического давления на криволинейную поверхность связано с геометрическим сложением составляющих сил.
Рассмотрим один из примеров решения этой задачи, который заключается в предварительном определении составляющих полного давления по нескольким направлениям (рис. 2.24).
Рис. 2.24
Выберем оси координат. Искомую силу F гидростатического давления на некоторую криволинейную поверхность А разложим по направлениям осей координат на три взаимно перпендикулярные составляющие 
Для отыскания силы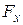 
, действующей по направлению оси ОХ, заданную криволинейную поверхность А спроектируем на плоскость проекций В, нормальную к оси ОХ и рассмотрим равновесие жидкого тела, ограниченного с одной стороны поверхностью А и с другой стороны – её проекцией 
. Составим уравнение равновесия в проекциях всех сил, приложенных к этому телу, на ось ОХ. Силы давления окружающей жидкости на боковые поверхности данного тела нормальны к оси ОХ и их проекции равны нулю. Так же не войдут в уравнение равновесия нормальные к оси ОХ составляющие силы 
и сила тяжести данного жидкого тела.
Тогда уравнение равновесия составится из проекций только двух сил
, (2.102)
где 
– сила гидростатического давления на плоскую фигуру .
(2.103)
Следовательно, составляющая силы гидростатического давления на криволинейную поверхность в направлении оси ОХ равна сила давления жидкости на её вертикальную проекцию, нормальную к оси ОХ. Так как эта проекция является плоской фигурой, то сила 
в соответствии с ранее полученной формулой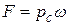 
найдётся как произведение её площади на гидростатическое давление в её центре тяжести, т.е.
(2.104)
где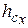 
- глубине расположения центра тяжести площади.
Другая горизонтальная составляющая 
определится аналогичным образом. Для этого криволинейную поверхность следует спроектировать на плоскости проекций ZOX и рассмотреть равновесие аналогичного жидкого тела в проекциях всех сил на ось ОУ.
В конечном счёте получим
(2.105)
где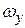 
– площадь проекции; 
– глубина погружения центра тяжести площади .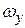
Для нахождения вертикальной составляющей силы 
заданную криволинейную поверхность спроектируем на плоскость свободной поверхности жидкости и рассмотрим равновесие жидкого тела, ограниченного снизу рассматриваемой поверхностью А, а сверху- её проекцией 
. Из всех сил, приложенных к этому телу, которое называется телом давления, на вертикальную ось OZ спроектируется только сила 
и сила тяжести тела давления G. Все остальные силы нормальны к оси OZ и в уравнение равновесия не войдут.
(2.106)
Откуда
(2.107)
где W - объём тела давления.
Равнодействующая сила гидростатического давления на криволинейную поверхность найдётся по формуле
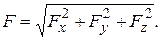(2.108)
Положение центра давления для криволинейных поверхностей может быть определено либо графическим, либо аналитическим способом по известным законам механики. При этом следует иметь ввиду, что составляющие силы 
в соответствии с условиями равновесия приложены по линиям действия соответствующих сил 
Линии действия горизонтальных сил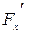 
и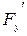 
приложенных к плоским фигурам, определяется с помощью формулы:
, (2.109)
, (2.110)
где 
– глубины центров давления соответственно сил; 
– центральные моменты инерций соответствующих плоских фигур 
относительно горизонтальных осей.
Линия действия вертикальной составляющей 
всегда проходит через центр тяжести тела давления W.
