Гидростатическим давлением называется внутренние напряжения сжатия в жидкости, возникающие под действием внешних сил.
Всякое жидкое тело в состоянии равновесия находится под воздействием двух категорий внешних сил: поверхностных и массовых.
Поверхностные силы – это силы, которые оказывают действие на поверхность жидкого тела, например, силы давления поршня или плунжера насоса, атмосферное давление и т. п.
Массовые, или объемные, силы – это силы тяжести, инерции и центробежные силы, которые в однородной жидкости распределены по всему объему жидкого тела. Величина элементарной массовой силы, приложенной к частичке жидкости, пропорциональна массе этой частицы.
Силы внутреннего трения в покоящейся жидкости не проявляются.
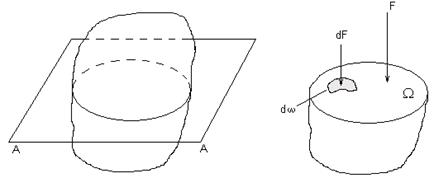
Рис. 2.1
Возьмем жидкое тело, находящееся в состоянии покоя и мысленно разделим его по плоскости А-А на две части. Верхнюю часть отбросим, а ее силовое воздействие на нижнюю часть заменим силой F (рис.2.1). Сила F, приложенная к площади W, разделяющей верхнюю и нижнюю части жидкого тела, называется силой гидростатического давления.
При этом следует иметь ввиду, что нижняя часть воздействует на верхнюю с силой равной по величине F, но противоположной по направлению.
Величина среднего гидростатического давления определяется величиной силы, приходящейся на единицу площади, т. е.
. (2.1)
Величина гидростатического давления в какой-либо точке площади W, определяется отношением элементарной силы dF, приложенной к элементарной площадке dw, расположенной в области данной точки.
. (2.2)
Единицей измерения гидростатического давления в системе СИ является Паскаль. 1 Па = 1 Н/м2.
Гидростатическое давление обладает двумя основными свойствами.
Первое свойство гидростатического давления.
Гидростатическое давление действует всегда по внутренней нормали, направленной к площадке действия. Это положение может быть доказано методом от противного. Предположим, что вектор гидростатического давления Р направлен не по нормали, а по наклонной линии (рис.2.2). Разложим его на нормальную Рн и касательную Рк составляющие. Нормальные составляющие верхней и нижней частей тела уравновесятся, а касательные составляющие вызовут смещение одной части жидкости относительно другой, что противоречит состоянию покоя. Следовательно, гидростатическое давление может быть направлено лишь по нормали к площадке действия.
Теперь предположим, что вектор Р направлен не по внутренней, а по внешней нормали (рис. 2.3). Так как жидкость не обладает способностью воспринимать растягивающие усилия, то произойдет разрыв жидкого тела, что также противоречит состоянию покоя и физическим свойствам жидкости. Поэтому и это предположение исключается.
Из рассмотренного следует, что гидростатическое давление, будучи всегда направленным внутрь жидкости, является давлением сжимающим.
Второе свойство гидростатического давления.
В любой точке внутри жидкости гидростатическое давление одинаково по всем направлениям и не зависит от угла наклона площадки, на которую оно действует в данной точке.
Для доказательства этого свойства выделим в неподвижной жидкости элементарный объем в форме прямоугольной призмы с ребрами, параллельными координатным осям и соответственно равным dx, dy, dz (рис.2.4)
Рис.2.4.
Для наглядности сделаем проекцию призмы на координатные оси Оx и Оz. Пусть вблизи выделенного объема на жидкость действует единичная массовая сила, составляющие которой равны X, Y и Z.
Обозначим через Pк гидростатическое давление, действующее на грань, нормальную к оси Ox, через Py давление на грань, нормальную к оси Oy и т. д. Гидростатическое давление, действующее на наклонную грань обозначим через Pn, а площадь грани через dw. Все эти давления направлены по нормалям к соответствующим площадкам.
Составим уравнение равновесия выделенного объёма жидкости сначала в направлении оси Ox
, (2.3)
где 
– направление действия массовой силы.
Решаем:
, (2.4)
, (2.5)
(угол a образован нормально Pn и осью Ox)
, 
(2.6)
(X – единичная массовая сила вдоль его объёма).
Масса тетраэдра равна произведению его объёма dW на плотность r, т.е.
. (2.7)
Тогда,
. (2.8)
Запишем теперь уравнение равновесия:
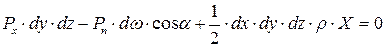, (2.9)
Разделим все члены уравнения (2.9) на площадь yOz (т.е. на dydz)
Будем иметь:
. (2.10)
При стремлении размеров к нулю, последний член уравнения (2.10), содержащий множитель dx, будет так же стремиться к нулю, а давления Px и Pn будут оставаться величинами конечными.
Следовательно, в пределе мы получим:
(2.11)
или
. (2.12)
Аналогично составляя уравнения равновесия вдоль осей Oy и Oz, после таких же рассуждений получим:
, 
(2.13)
или
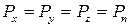. (2.14)
Так как размеры прямоугольной призмы dx, dy, dz были взяты произвольно, то и наклон площадки dw произволен, и, следовательно, в пределе при стягивании призмы в точку давление в этой точке по всем направлениям будет одинаково.
Рассмотренное свойство давления в неподвижной жидкости имеет место так же при движении идеальной жидкости. При движении же реальной жидкости возникают касательные напряжения, вследствие чего давление в реальной жидкости указанным свойством не обладает.
