ГИДРАВЛИКА,
ГИДРОПРИВОД И ГИДРОСИСТЕМЫ
Учебное пособие
Воронеж 2006
СОДЕРЖАНИЕ
Стр.
Введение ……………………………………………………………………………3
1. Физические свойства жидкостей ……………………………………………. 5
2. Гидростатика ………………………………………………………………….13
2.1. Гидростатическое давление и его свойства…………………………13
2.2. Общие дифференциальные уравнения гидростатики (Эйлера)……17
2.3. Интегрирование уравнений Эйлера
контактный теплообмен в соединениях …………………………….19
2.4. Основное уравнение гидростатики…………………………….…….20
2.5. Поверхности равного давления…….………………………………...21
2.6. Относительный покой жидкости……………………………………..22
2.7. Классификация давлений……………………………………………..25
2.8. Единицы измерения давлений………………………………………..26
2.9. Приборы для измерения давлений……………………………………27
2.10. Гидростатический и пьезометрический напоры…………………...32
2.11. Закон Паскаля и его применение……………………………………39
2.12. Давление жидкости на плоские поверхности………………………40
2.12.1. Давление жидкости на плоскую горизонтальную поверхность...40
2.12.2. Давление жидкости на наклонную поверхность…………………41
2.12.3. Определение положения центра давления………………………..43
2.12.4. Эпюры гидростатического давления на плоские поверхности….45
2.13. Давление жидкости на криволинейные поверхности……………...48
2.13.1.Определение равнодействующей суммарного гидростатичес-
кого давления……………………………………………………....48
2.13.2.Эпюры гидростатического давления на криволинейные
поверхности………………………………………………………...51
2.14. Закон Архимеда………………………………………………………53
3. Гидродинамика..………………………………………………………………..55
3.1. Задачи гидродинамики…………………………………….………......55
3.2.Основные понятия. Модель движения………………………………..55
3.3. Уравнения неразрывности для элементарной струйки
и для потока…………………………………………………………....60
3.4. Уравнение Бернулли для элементарной струйки идеальной
несжимаемой жидкости…………………………………………….....62
3.5. Формы механической энергии. Преобразование энергии…………..65
3.6. Уравнение Бернулли для элементарной струйки вязкой
Жидкости…………………………………………………………….....67
3.7. Уравнение Бернулли для потока вязкой жидкости……………….…69
3.8. Уклоны: геометрический, пьезометрический и гидравлический…..72
3.9. Основное уравнение равномерного движения жидкости.
Формула Шези…………………………………………………………74
3.10. Два режима движения вязкой жидкости……………………………76
3.10.1. Ламинарный режим движения жидкости в трубах………………79
3.10.2. Турбулентный режим движения жидкости…………………...….82
3.10.3. Силы трения и закон распределения скоростей при
турбулентном режиме…………………………...…………………85
3.11. Коэффициент гидравлического трения……………………………..87
3.12. Гидравлические потери………………………………………………89
3.12.1. Местные потери напора……………………………………………90
3.13. Коэффициент сопротивления системы. Характеристика системы. 94
3.14. Гидравлический расчёт трубопроводов…………………………….96
3.15. Гидравлический удар в трубах………………………………………99
4. Гидропривод ……………………………………………………………..….....102
4.1. Назначение. Основные элементы схемы………….………..……….102
4.2. Классификация гидропривода……………………………………….107
4.3. Насосы…………………………………………………………….......110
4.3.1. Простой поршневой насос………………………………………...111
4.3.2. Радиально-поршневые насосы….………………………………...115
4.3.3. Аксиально-поршневые насосы……………………………….…...118
4.3.4. Пластинчатые насосы……………………………………………...121
4.3.5. Шестерённые насосы……………………………….…………...…123
4.4. Гидроцилиндры………………………………………………...…….127
4.5. Гидрораспределители………………………………………………...132
4.5.1. Золотниковые гидрораспределители……………………………...133
4.5.2. Крановые (пробковые) гидрораспределители…………………....137
4.6. Гидроклапаны……………………………………………………...…138
4.6.1. Напорные гидроклапаны…………………………………...……...139
4.6.2. Редукционные гидроклапаны…………………………….………..141
4.6.3. Обратные гидроклапаны…………………………………………...143
4.6.4. Ограничители расхода……………………………………..………143
4.6.5. Делители потока………………………………...………………….143
4.7. Дроссели………………………………………………………………144
4.8. Регулирование гидропривода………………………………………..148
4.9. Вспомогательные устройства гидропривода…………………….....149
5. Библиографический список ……………………………………………...….150
Введение
Гидравлика – это прикладная часть гидромеханики, которая изучает законы равновесия и движения жидкости и разрабатывает методы использования этих законов в инженерной практике.
По мере усложнения технических задач произошло слияние гидравлики и гидромеханики в единую науку – техническую гидромеханику. Вводную, наиболее общую часть этой науки в силу традиций часто продолжают именовать гидравликой. Техническая гидромеханика – наука развивающаяся. Этому свидетельствует бурное развитие в последние десятилетия таких специальных разделов, как электромагнитная гидродинамика, теория гидромашин, гидропривод.
Современная гидравлика с прикладной точки зрения изучает законы различных состояний покоя и многообразных форм движения не только для воды, но и применительно к множеству других технических жидкостей.
Гидравлика делится на две части: гидростатика и гидродинамика.
Гидростатика изучает законы покоя и равновесия жидкостей, законы распределения давления внутри жидкости и её действие на погруженные в жидкость тела.
Гидродинамика изучает законы движения жидкости в трубопроводах и в открытых потоках.
Знание основ гидравлики необходимо для гидравлического расчёта трубопроводов различного назначения – для воды, масел, горючего и других жидкостей. На основании законов гидравлики определяется сила давления жидкости на стенки трубопроводов, цистерн, бензобаков и других ёмкостей. Производится расчёт их прочности, деформаций и устойчивости.
Основные законы гидравлики чрезвычайно широко используются в теории расчёта и эксплуатации всех гидравлических машин и гидравлического привода.
Гидравлическими машинами называются механические устройства, принцип работы которых основан на силовом взаимодействии их рабочих органов с жидкостью. К гидравлическим машинам относятся насосы, гидравлические двигатели, гидравлические прессы, подъёмники и др. Насосы, например, в качестве вспомогательных устройств входят в состав тепловых двигателей, в различных машинах они служат для подачи в рабочие органы топлива, масла, воды, воздуха, и других жидкостей.
Гидравлический привод невозможно представить без применения гидравлических машин.
Гидравлический привод представляет собой совокупность устройств, которые служат для передачи механической энергии и преобразования движения при помощи жидкости. Например, поступающая в систему гидравлического привода внешняя механическая энергия с помощью него преобразуется в гидравлическую энергию рабочей жидкости. Последняя подаётся, например, по системе трубопроводов в гидравлический двигатель – гидромотор или силовой цилиндр – где энергия жидкости преобразуется в механическую энергию.
Гидравлические приводы различных типов нашли широкое применение в качестве силовых трансмиссий, в системах управления рабочими органами станков, различных машин и технологических линий. Поэтому, с ростом автоматизации современного производства инженерам просто необходимо знание теории гидравлических машин для правильного выбора и эффективной эксплуатации насосов, турбин, гидравлических прессов, систем гидравлического привода и других гидравлических машин и устройств.
Таким образом, изучение настоящего курса имеет очень большое значение в профессиональной подготовке инженера по автоматизации лесопромышленного комплекса.
Физические свойства жидкостей
Жидкостью называют физическое тело, обладающее свойством текучести, т.е. способностью неограниченно изменять свою форму под действием сколь угодно малых сил. В отличие от газа, жидкость мало изменяет свою плотность при изменении давления.
Жидкости делятся на капельные и газообразные. Капельная жидкость в сосуде принимает форму сосуда и образует свободную поверхность. Газообразная жидкость принимает форму сосуда и заполняет весь его объём.
Капельные жидкости, такие, как вода, керосин, бензин, нефть, ртуть и другие, в состоянии невесомости образуют капли. Газообразные жидкости – воздух и другие газы в состоянии невесомости капель не имеют.
Гидравлика занимается изучением капельных жидкостей, однако её основные законы можно применять и при изучении газов, находящихся в состоянии покоя или движущихся со скоростями до 80 – 100 м/с.
В дальнейшем под термином «жидкость» будем подразумевать главным образом капельную жидкость, а так же газообразную жидкость при малом изменении её плотности.
Жидкости обладают рядом свойств, присущих всем физическим телам – массой, весом и другие, а так же свойствами, характерными только для жидкостей, знание которых необходимо при рассмотрении последующего материала.
Плотность жидкости – это количество массы m, заключённое в единице объёма W однородного жидкого тела
. (1.1)
Единицей измерения плотности в системе СИ является 1 кг/м3. Например, среднее значение плотности для бензина 
=710 кг/м3, для нефти =800 кг/м3, плотность дистиллированной воды при 4оС и нормальном барометрическом давлении, =1000 кг/м3, ртуть имеет плотность =13600 кг/м3. С ростом давления, плотность жидкостей увеличивается, а при возрастании температуры, как правило, уменьшается.
Удельный вес – это отношение веса жидкости G, т.е. силы тяжести, действующей на жидкость, к её объему W
. (1.2)
В системе СИ единицей удельного веса является 1 Н/м3. В случаях, когда удельный вес измеряется в кГс/м3 (система МКГСС), численные значения плотности и удельного веса совпадают. Например, удельный вес чистой дистиллированной воды при температуре 4оС и нормальном барометрическом давлении составляет 
= 9810 Н/м3. Обычная пресная вода (речная, колодезная, водопроводная) за счёт растворимых в ней различных веществ несколько тяжелее дистиллированной воды. Однако это различие невелико. Поэтому в практике гидравлических расчётов удельный вес пресной воды без существенной погрешности принимается равным удельному весу дистиллированной воды. Удельный вес морской воды в зависимости от её солёности на 2..3 % выше удельного веса дистиллированной воды.
Между плотностью и удельным весом существует прямая взаимосвязь. Удельный вес может быть выражен произведением плотности на ускорение силы тяжести g:
. (1.3)
Откуда плотность жидкости или какого либо другого вещества может быть определена из соотношения его удельного веса к ускорению силы тяжести:
. (1.4)
Сжимаемость – это свойство жидкости уменьшать свой объём под воздействием внешних сил. Несмотря на это, подвижность молекул в жидкостях невелика, жидкости удаётся заметно сжать только с помощью очень больших давлений. Жидкости обладают ничтожной сжимаемостью. Сжимаемость жидкости характеризуется коэффициентом объёмного сжатия 
.
Он представляет собой относительное уменьшение объёма жидкости при повышении давления на одну единицу
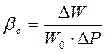, (1.5)
где 
- начальный объём жидкого тела, 
- абсолютное уменьшение объёма жидкости, 
- полное приращение давления.
Размерность коэффициента 
в системе СИ - м2/Н или 1/Па.
Капельные жидкости в отличие от газов оказывают значительное сопротивление сжимающим силам и потому имеют очень малые значения коэффициентов объёмного сжатия. Например, для пресной воды 
м2/Н.
По причине малости жидкостей последние считаются практически несжимаемыми, и во многих инженерных расчётах свойством сжимаемости жидкости пренебрегают.
Величина, обратная называется модулем упругости Е:
. (1.6)
Для пресной воды 
Н/м2.
Температурное расширение – это свойство жидкости изменять свой объём при изменении температуры. Это свойство количественно характеризуется коэффициентом температурного расширения 
, который выражает относительное увеличение объёма жидкости при повышении её температуры на 1оС
. (1.7)
Здесь - начальный объём жидкого тела, - полное приращение объёма жидкости, 
- повышение температуры. Единица измерения – 
.
Коэффициент температурного расширения воды увеличивается с возрастанием давления и температуры, для большинства других капельных жидкостей, с увеличением давления уменьшается. Величина у капельных жидкостей относительно мала, и это позволяет во многих практических расчётах пренебрегать температурным расширением. Например, для воды в пределах температур от 10 до 20оС и давлении в 1 атмосферу равен 0.00015 1/ оС. Для нефти и нефтепродуктов = 0.00060 … 0.00085 1/ оС.
Вязкость или внутреннее трение – это свойство жидкости оказывать сопротивление при относительном смещении её слоёв. Сопротивление среды при сдвиге связано с возникновением касательных напряжений.
Впервые гипотезу о внутреннем трении в жидкостях сформулировал Исаак Ньютон (1687год).
Рис. 1.1 Относительное смещение двух соседних слоев жидкости
Сущность этой гипотезы состоит в следующем: сила внутреннего трения, возникающая между соседними слоями жидкости a и b (рис.1.1), при их относительном смещении, прямо пропорциональна скорости движения и площади их взаимодействия, обратно пропорциональна расстоянию между слоями и зависит от рода жидкости, т.е.
, (1.8)
где Т – сила сопротивления сдвигу слоёв, 
- поверхность, на которой происходит силовое взаимодействие, du – разность скоростей движения соседних слоёв, dh – расстояние между слоями жидкости,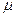 
- коэффициент пропорциональности, характеризующий вязкостные свойства данной жидкости.
Впервые гипотеза Ньютона была официально подтверждена профессором Н.П.Петровым (1883 г.), и с этой поры зависимость (1.8) стала именоваться законом Ньютона для трения жидкости.
Разделим правую и левую части формулы (1.8) на и обозначим Т/ 
= t, тогда
, (1.9)
где t - удельная сила трения, или касательные напряжения, Н/м2.
Эта зависимость называется формулой проф. Петрова. Отношение 
называется градиентом скорости, который показывает изменение скорости смещения слоёв жидкости на единицу расстояния в поперечном направлении. Из формулы Ньютона видно, что при нулевой разнице скоростей (du = 0, например, в покоящейся жидкости) силы внутреннего трения не проявляются.
Коэффициент пропорциональности 
в приведённых формулах характеризует абсолютную, или динамическую вязкость жидкости. Более вязким жидкостям соответствует более высокие значения .
Размерность коэффициента в системе СИ – Паскаль-секунда (Па × с) = Н × с/м2 = кг/(Па × с). До 1980 года использовалась единица – Пуаз (П).1 П = 0.1 Па × с (в честь французского исследователя Ж. Пуазейля).
Кинематическим коэффициентом вязкости 
называется отношение динамического коэффициента вязкости к плотности данной жидкости, т.е.
. (1.10)
Единицей измерения u в системе СИ является м2/с. До 1980 года в качестве единицы измерения u использовались стоксы (в честь английского физика Д. Стокса). 1 Ст = 10-4 м2/с.
Величина, обратная коэффициенту динамической вязкости называется текучестью.
При слоистом движении капельной жидкости вязкость проявляется благодаря силам молекулярного сцепления. С увеличением температуры эти силы уменьшаются, поэтому вязкость существенно падает.
Изменение вязкости происходит и при изменении давления на жидкость. Однако в пределах давлений до 10,1 МПа (100 атмосфер) это изменение незначительно и в практических расчётах им обычно пренебрегают.
Установление числовых значений коэффициентов вязкости различного рода жидкостей производится опытным путём с помощью приборов вискозиметров (от франц. v iscosite – вязкость). Существует множество типов вискозиметров, основанных на различных принципах действия. В нашей стране для исследований жидкостей более вязких, чем вода применяется вискозиметр Энглера. Он представляет собой латунный бачок ёмкостью 200 см3 (рис.1.2). Для выпуска исследуемой жидкости сферическое дно бачка снабжено отверстием диаметром 2,8 мм. В каждом случае время истечения исследуемой жидкости сравнивается со временем истечения дистиллированной воды, взятой в том же объеме.
Рис. 1.2 Вискозиметр Энглера
Условная вязкость исследуемой жидкости (“ ВУ ”), выраженная в градусах Энглера (оЕ), находится из соотношения:
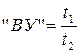, (1.11)
где t1 – время истечения исследуемой жидкости в объеме 200 см3, t2 – время истечения дистиллированной воды, взятой в том же объеме.
Вязкость жидкости в градусах Энглера обычно определяется при температуре 20 оС. Для поддержания постоянной температуры в течение всего опыта вискозиметр снабжен водяной ванной, обогрев которой до заданной температуры производится с помощью газовой горелки или электрического подогревателя.
Для пересчета градусов Энглера или градусов “ ВУ ” в стоксы пользуются эмпирической формулой Уббеллоде
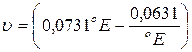. (1.12)
Динамический коэффициент вязкости в соответствии с формулой (1.10) определяется как
. (1.13)
Кроме рассмотренных физических свойств жидкостей в некоторых практических задачах для капельных жидкостей приходится учитывать давление насыщенных паров, растворимость газов, пенообразование, поверхностное натяжение, капиллярность. Численные величины этих параметров при необходимости могут быть найдены в справочниках физических или теплофизических величин.
Жидкость, обладающая всем комплексом рассмотренных выше физических свойств, является реальной.
С точки зрения гидравлики одним из важнейших свойств реальной жидкости является вязкость, поэтому реальные жидкости часто называют еще вязкими или ньютоновскими (поскольку проявление сил вязкости описывается законом Ньютона).
Поведение реальной жидкости при разнообразных внешних условиях может оказаться весьма сложным, труднодоступным для изучения и математического описания (например, бурный ручей). Поэтому для получения приближенных решений, зачастую подлежащих последующему уточнению, в гидравлике с успехом применяется модель так называемой совершенной или идеальной жидкости.
Совершенной называется условная абсолютно подвижная (т.е. лишенная вязкости) абсолютно несжимаемая, не изменяющая объема с изменением температуры жидкость, абсолютно неспособная сопротивляться разрыву.
Для совершенной жидкости: 
.
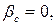
В совершенной жидкости не может существовать ни касательных, ни растягивающих напряжений.
Кроме вязкой и совершенной жидкостей в гидравлике приходится иметь дело с так называемым аномальными или неньютоновскими жидкостями, т. е. такими, которые не подчиняются закону вязкого трения Ньютона.
Опытным путем установлено, что движение неньютоновских жидкостей начинается только после того, как касательные напряжения достигнут некоторого предельного минимального значения 
(так называемое начальное напряжение сдвига). При меньших напряжениях эти жидкости не текут, а испытывают только упругие деформации.
Для этого типа жидкостей 
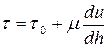. (1.14)
Эта формула получена Бингемом, поэтому неньютоновские жидкости называют бингемовскими.
Примером аномальных жидкостей могут служить коллоиды (студни), нефтепродукты при температуре, близкой к температуре застывания, густые глинистые и грязевые растворы и т. п.
Гидростатика
