Для изучения методов решения нелинейных уравнений важным является знание приближенных графических методов их решения.
Действительные корни уравнения F(x)=0 приближенно можно определить как абсциссы точек пересечения функции y=F(x) с осью Ох.
Если уравнение F(x)=0 не имеет близких между собой корней, то этим способом, как показано на рис.4.2, его корни отделяются.
Рисунок 4.2 – Приближенное определение корней уравнения
На практике часто бывает выгоднее это уравнение заменить равносильным ему уравнением
j(x)=y(x),
где функции j(x) и y(x) более просты, чем функция F(x).
Тогда, построив графики функций
y=j(x)
и
y=y(x),
искомые корни получим как абсциссы точек пересечения этих графиков.
Например, необходимо графически решить уравнение x lgx=1.
Запишем его в виде:
.
Построив кривые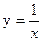 
и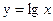 
, как показано на рис.4.3, приближенно найдем единственный корень уравнения х» 2,5.
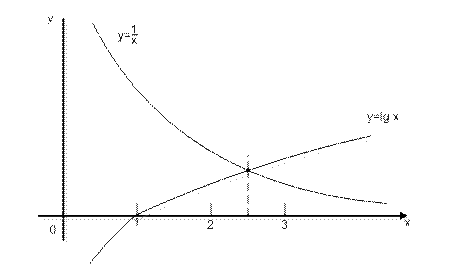
Рисунок 4.3 – Графическое решение уравнения x lgx=1
Нахождение корней уравнения упрощается, если одна из функций y=j(x) или y=y(x) линейная, т.е., например, j(х)=ax+b. Тогда корни находятся, как абсциссы точек пересечения кривой y=y(x) и прямой y=ax+b. Именно такой графический способ нам потребуется использовать при изучении, например, метода последовательных приближений.
Хотя графические методы решения уравнений весьма удобны и сравнительно просты, но они, как правило, применимы лишь для грубого определения корней. Особенно неблагоприятным в смысле потери точности является случай, когда линии пересекаются под очень острым углом и практически сливаются по некоторой дуге.
Метод половинного деления
Пусть дано уравнение F(x)=0, где функция F(x) непрерывна в области своего существования. Требуется найти корень этого уравнения, что графически представляется точкой пересечения графика функции F(x) и оси Х (рис.4.4).
Рисунок 4.4 – Иллюстрация метода половинного деления
Алгоритм метода состоит из следующих операций:
Сначала вычисляются значения функции в точках, расположенных через равные интервалы на оси Х. Это делается до тех пор, пока не будут найдены два последовательных значения функции F(a) и F(b), имеющие противоположные знаки. Если функция непрерывна, изменение знака указывает на существование корня.
Затем по формуле 
вычисляется среднее значение Х в интервале значений [а,b] и находится значение функции F(с). Если знак функции F(c) совпадает со знаком F(a), то в дальнейшем вместо F(a) используется F(c). Если же F(c) имеет знак, противоположный знаку F(a), т.е. ее знак совпадает со знаком F(b), то F(b) заменяется на F(c).
Далее находим (для нашего случая):
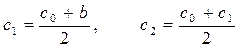
и так далее.
В результате интервал, в котором заключено значение корня, сужается. Если F(c) достаточно близко к нулю, процесс заканчивается, в противном случае он продолжается.
Часто применяется другая оценка сходимости:
|cn+1 – cn|<ε
Величина F(а) определяется лишь один раз, поскольку нам нужен только знак функции F(х) на левой границе, и он в процессе итераций не меняется.
Метод половинного деления не обладает высокой вычислительной эффективностью. Однако с увеличением числа итераций он обеспечивает получение все более точного приближенного значения корня. После того, как впервые найден интервал, в котором заключен корень, его ширина после N итераций убывает в 2N раз.
