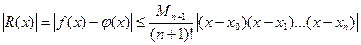Интерполяционная формула Ньютона

 

Довольно распространенным методом интерполирования является метод Ньютона. Интерполяционный полином для этого метода имеет вид:

P_n(x) = a₀ + a₁(x-x₀) + a₂(x-x₀)(x-x₁) +... + a_n(x-x₀)(x-x₁)...(x-x_n-1).

Задача состоит в отыскании коэффициентов a_i полинома P_n(x). Коэффициенты находят из уравнения:

P_n(x_i) = y_i, i = 0, 1,..., n,

позволяющего записать систему:

a₀ = y₀;

a₀ + a₁(x₁ - x₀) = y₁;

a₀ + a₁(x₂ - x₀) + a₂(x₂ - x₀)(x₂ - x₁) = y₂;

- - - - - - - - - - - - - - - - - - - - - - - - - - - -

a₀ +... + a_n(x_n - x₀)(x_n - x₁)... (x_n - x_n-1) = y_n;

Используем метод конечных разностей. Если узлы x_i заданы через равные промежутки h, т.е.

x_i+1 - x_i = h,

то в общем случае x_i = x₀ + i×h, где i = 1, 2,..., n. Последнее выражение позволяет привести решаемое уравнение к виду

y₀ = a₀;

y₁ = a₀ + a₁×h;

y₂ = a₀ + a₁(2h) + a₂(2h)h;

- - - - - - - - - - - - - - - - - - -

y_i = a₀ + a₁×i×h + a₂×i×h[(i-1)h] +... + a_i×i!×hⁱ,

откуда для коэффициентов получаем

a₀ = y₀;

,

где Dу₀ – первая конечная разность.

Продолжая вычисления, получим:

где D²у₀ - вторая конечная разность, представляющая собой разность разностей. Коэффициент а_i можно представить в виде:

.

Поставляя найденные значения коэффициентов а_i в значения для P_n(x), получим интерполяционный полином Ньютона:

Преобразуем формулу, для чего введем новую переменную , где q – число шагов, необходимых для достижения точки х, двигаясь из точки х₀. После преобразований получаем:

 

 

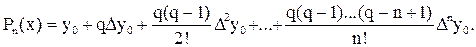
Полученная формула известна как первая интерполяционная формула Ньютона, или формула Ньютона для интерполирования "вперед". Ее выгодно использовать для интерполирования функции y = f(x) в окрестности начального значения х – х₀, где q мало по абсолютной величине.

Если записать интерполяционный многочлен в виде:

 

 

то аналогичным образом можно получить вторую интерполяционную формулу Ньютона, или формулу Ньютона для интерполирования "назад":

 

.

 

Ее обычно используют для интерполирования функции вблизи конца таблицы.

При изучении данной темы необходимо помнить, что интерполяционные многочлены совпадают с заданной функцией f(x) в узлах интерполяции, а в остальных точках, в общем случае, будут отличаться. Указанная ошибка дает нам погрешность метода. Погрешность метода интерполяции определяется остаточным членом, который для формул Лагранжа и Ньютона одинаков и который позволяет получить следующую оценку для абсолютной погрешности:

 

где

Если интерполирование осуществляется с одинаковым шагом, то формула для остаточного члена видоизменяется. В частности, при интерполировании "вперед" и "назад" по формуле Ньютона выражение для R(x) несколько отличаются друг от друга.

Анализируя полученную формулу, видно, что погрешность R(x) представляет собой, с точностью до постоянной произведение двух множителей, из которых один, f⁽ⁿ⁺¹⁾(x), где x лежит внутри [x₀, x_n], зависит от свойств функции f(x) и не поддается регулированию, а величина другого,

определяется исключительно выбором узлов интерполирования.

При неудачном расположении этих узлов верхняя граница модуля |R(x)| может быть весьма большой. Поэтому возникает задача о наиболее рациональном выборе узлов интерполирования x_i (при заданном числе узлов n) с тем, чтобы полином П_n+1(х) имел наименьшее значение.

Эта задача была решена русским математиком П.Л. Чебышевым, который доказал, что наилучший выбор в указанном смысле узлов интерполирования на отрезке [a, b] дается формулой

где

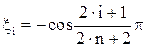, i = 0,1,…,n

 

- нули так называемого полинома Чебышева:

 

.

В этом случае мы будем иметь:

.

Отметим, что эти узлы не являются равноотстоящими, а сгущаются около концов отрезка [a, b].