1.Повторить следующие методы решения СЛАУ:
- итерационный метод Якоби;
- итерационный метод Гаусса-Зейделя;
- прямой метод Гаусса;
2.Обратить внимание на достаточные условия сходимости метода Гаусса-Зейделя.
3.Составить граф-схемы алгоритмов:
- итерационного метода Якоби;
- итерационного метода Гаусса-Зейделя;
- прямого метода Гаусса.
4.По граф-схемам алгоритмов составить программы численного решения СЛАУ.
Задания для практической работы
1.Решить заданную таблицей 1 систему из двух уравнений с двумя неизвестными любым точным методом.
2.Подготовить СЛАУ к решению методом Гаусса-Зейделя и проделать 4-5 итераций.
3.Представить геометрическое истолкование процесса.
4.Используя метод Якоби, проделать то же число итераций.
5.Сравнить результаты пунктов 2) и 4) с 1) и сделать выводы о скорости сходимости этих итерационных процессов к решению задачи.
Таблица 1
| №1 х – 3у = - 5 2х + у = 4 | №2 х + 2у = 3 3х + у = -1 | №3 х +3у = -5 2х – у = 4 | №4 2х – 3у = 4 х + у = -3 | №5 3х – у = 3 х + 2у = 8 |
| №6 х – 2у = -8 -3х + у = 9 | №7 х – 2у = 8 4х + у = 5 | №8 х – 4у = 10 -2х + у = 1 | №9 х – 3у = -1 2х + у = 5 | №10 х + 2у = 11 2х – у = 2 |
| №11 х + 3у = -1 3х + у = 5 | №12 х + 3у = 1 2х – у = -5 | №13 х + 2у = 7 3х – у = 7 | №14 х – 2у = 7 -3х+у = -11 | №15 х – 2у = -7 4х +у = -10 |
| №16 х + 2у = 3 3х + у = -1 | №17 2х – 3у = 4 х + у = -3 | №18 х – 2у = -8 -3х + у = 9 | №19 х – 4у = 10 -2х + у = 1 | №20 х + 2у = 11 2х – у = 2 |
| №21 х – 3у = - 5 2х + у = 4 | №22 х +3у = -5 2х – у = 4 | №23 3х – у = 3 х + 2у = 8 | №24 х – 2у = 8 4х + у = 5 | №25 х – 3у = -1 2х + у = 5 |
Задания к лабораторной работе
1.Решить подготовленный вариант СЛАУ методом Якоби с точностью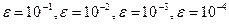 
. Зафиксировать число итераций, произвести проверку полученного решения.
2. Решить подготовленный вариант СЛАУ методом Гаусса-Зейделя с точностью 
.Зафиксировать число итераций, произвести проверку полученного решения.
3. Оценить эффективность методов по скорости сходимости итерационных процессов.
4. Решить СЛАУ методом Гаусса. Сравнить результаты решения п. 1,2 с решением п. 4.
5. Результаты решения и сравнительные характеристики методов представить в таблице.
6. Представить выводы по работе.
Номер варианта соответствует порядковому номеру студента по списку преподавателя.
При решении задач использовать программное обеспечение, разработанное в процессе самостоятельной подготовки, а также программы из пакета лабораторных прикладных программ.
Варианты задания
Вариант №1,12 Вариант №2,13
Вариант №3,14 Вариант №4,15
Вариант №5,16 Вариант №6,17
Вариант №7,18 Вариант №8,19
Вариант №9,20 Вариант №10,21
Вариант №11,22
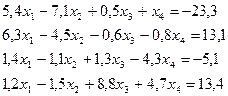
Содержание отчета
1. Цель работы.
2. Краткие теоретические сведения о методах численного решения СЛАУ, граф-схемы алгоритмов.
3. Листинги разработанных программ.
4. Таблицы результатов численного решения СЛАУ с указанием количества итераций для каждого метода при заданной точности решения.
5. Выводы по лабораторной работе, подтвержденные данными таблицы, графиками и расчётами, сравнительные характеристики методов.
Контрольные вопросы
1. Дать определение СЛАУ. Какие СЛАУ называются вырожденными? Какие СЛАУ называются плохо обусловленными?
2. Перечислите известные Вам численные методы решения СЛАУ.
3. Чем отличаются прямые (конечные) методы от итерационных (бесконечных) методов решения СЛАУ?
4. При каких условиях сходится (расходится) итерационный процесс метода Гаусса-Зейделя.
5. Расскажите, чем отличается метод Якоби от метода Гаусса-Зейделя.
6. Ранжируйте численные методы решения СЛАУ по скорости сходимости итерационного процесса к решению системы.
7. Нарисуйте блок-схемы алгоритмов методов решения СЛАУ.
Лабораторная работа №2
ЧИСЛЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ
ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Пусть функция f(х) задана на некотором отрезке [а; b]. Рассмотрим задачу вычисления ее определенного интеграла 
. Если для f(х) известна первообразная F(х), то интеграл может быть вычислен точно по основной формуле интегрального исчисления — формуле Ньютона-Лейбница:
.
Однако первообразная лишь для узкого класса функций выражается через элементарные функции, причем нередко ее отыскание связано с очень громоздкими вычислениями. Кроме того, возможна ситуация, когда подынтегральная функция задана не аналитически, а таблично или графически. Поэтому для вычисления определенного интеграла часто приходится прибегать к различным приближенным формулам. Довольно просто эти формулы можно получить, исходя из геометрического смысла определенного интеграла:
если 
на [а; b], то 
– площадь криволинейной трапеции, ограниченной отрезком [а; b] оси Оx, кривой y=f(x) и прямыми x=a, x=b.
При приближенном вычислении криволинейную трапецию заменяют фигурой, площадь Sn которой вычисляется довольно просто. При этом фигура ограничена тем же отрезком [а; b]. Отсюда получают приближенную формулу
.
Цель лабораторной работы –
изучить:
- особенности численных методов интегрирования, в том числе метод интегрирования Гаусса;
- методические погрешности для каждого метода;
- вопрос о целесообразности увеличения числа интервалов интегрирования с учетом суммарной погрешности округления и ограничения;
- граф-схемы алгоритмов численного интегрирования методами прямоугольников, трапеций, Симпсона и Гаусса.
В результате проведения лабораторной работы студенты должны
знать:
- особенности применения и алгоритмы реализации различных методов численного интегрирования;
- влияние шага интегрирования на величину методической погрешности, погрешности округления и суммарной погрешности;
- методы повышения точности интегрирования за счет применения квадратурных формул гауссового типа.
уметь: выбирать и реализовывать методы численного интегрирования в соответствии с поставленной задачей, с требуемой точностью и трудоемкостью реализации алгоритмов вычислений.
Формула прямоугольников
Идея формулы прямоугольников заключается в том, что на малом отрезке [x0; x0+h] площадь криволинейной трапеции, как показано на рис.2.1, приближенно равна площади прямоугольника с основанием [x0; x0+h] и высотой, равной ординате в какой-то точке 
.
Рисунок 2.1 – Вычисление площади элементарной
криволинейной трапеции на отрезке h
Таким образом,
.
В зависимости от того, какую точку отрезка [x0; x0+h] выбирают в качестве 
, и получают разновидности формулы прямоугольников.
Разобьем отрезок [a; b] на n равных частей точками
a=x0, x1=x0+h, x2=x1+h, …, xi=xi-1+h, …, xn=xn-1+h=b, где 
.
На каждом частичном отрезке [xi-1; xi] заменим соответствующую криволинейную трапецию на прямоугольник, высоту которого можно выбрать по-разному.
1.1 Формула «левых» прямоугольников
Если выбрать в качестве высоты прямоугольника на каждом из отрезков [xi-1; xi], (
), ординату в левом конце, т. е. yi-1=f(xi-1), то криволинейная трапеция заменится на ступенчатую фигуру, площадь Sn которой можно принять за площадь трапеции. Верхняя граница этой ступенчатой фигуры изображена на рис. 2.2 сплошными линиями.
Рисунок 2.2 – Приближенное вычисление площади
криволинейной трапеции на отрезке [a; b]
Следовательно,
(1)
Полученную формулу называют формулой «левых» прямоугольников.
1.2 Формула «правых» прямоугольников
Если в качестве высоты прямоугольника выбрать ординату правого конца частичного отрезка, т. е. считать, что высота прямоугольника на отрезке [xi-1; xi] равна yi=f(xi), (), то для приближенного вычисления интеграла получим формулу «правых» прямоугольников:
(2)
(на рис. 2.2 штрихпунктирной линией обозначена ступенчатая фигура, составленная из «правых» прямоугольников).
1.3 Формула «средних» прямоугольников
Часто используется еще при расчетах так называемая формула «средних» прямоугольников или просто формула прямоугольников. Высотой прямоугольника, построенного на частичном отрезке, считают ординату, взятую в средней точке отрезка, т. е.
(получаемая ступенчатая фигура на рис. 2.2 заштрихована). Тогда
(3)
Формулы (1)—(3) можно использовать при аналитическом или графическом способе задания функции у = f (х), а формулы (1), (2) и при задании функции в виде таблицы с равноотстоящими узлами.
Формулу (3) можно записать в другом виде, более удобном для составления программ.
