Рассмотрим систему из 3-х уравнений с тремя неизвестными:
а11х1 + а12х2 + а13х3 = b1; (2.1)
а21х1 + а22х2 + а23х3 = b2; (2.2)
а31х1 + а32х2 + а33х3 = b3. (2.3)
Предположим, что а11¹0, а22¹0, а33¹0, и перепишем систему в виде:
 (2.4)
(2.4)
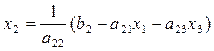 (2.5)
(2.5)
 (2.6)
(2.6)
В методе Якоби некоторое исходное приближение к решению этой системы, обозначенное как х1(0), х2(0), х3(0), одновременно используется с помощью выражений (2.4) – (2.6) для вычисления первого приближения х1(1), х2(1), х3(1) .Эти значения используются для вычисления второго приближения, и т.д. Процесс прекращается, когда достигается требуемая точность решения. В этом методе замена значений всех приближений производится одновременно (метод одновременных смещений).
В методе Гаусса-Зейделя также берется исходное приближение к решению системы (2.1) – (2.3), обозначенное как х1(0), х2(0), х3(0).
Подставим это решение в (2.4) и вычислим новое значение х1:
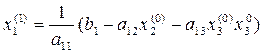 .
.
Используя полученное значение х1(1) и начальное значение х3(0), вычислим из (2.5) новое значение х2:
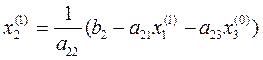 .
.
Используя значение х1(1) и х2(1), вычислим из (2.6) новое значение х3:
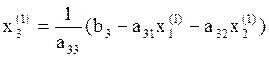 .
.
Этим заканчивается первая итерация. Теперь можно заменить исходные значения х1(0), х2(0), х3(0) на х1(1), х2(1), х3(1) и вычислить следующее приближение.
В общем случае k-ое приближение определяется формулами:
 (2.7)
(2.7)
Видно, что текущее значение неизвестных сразу же используется для последующих вычислений. Например, нельзя вычислить х2(k), пока не получено х1(k). Аналогично, для вычисления х3(k) необходимо сначала определить х1(k) и х2(k).
Метод Гаусса-Зейделя очень удобен для использования на ЭВМ.
Рассмотрим теперь систему из n уравнений с n неизвестными:
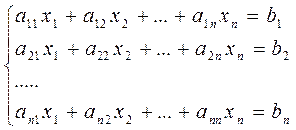 (2.8)
(2.8)
Мы по-прежнему предполагаем, что диагональные коэффициенты аii отличны от 0 для всех i. Тогда k-ое приближение к решению будет задаваться формулой:
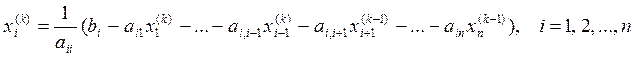 .
.
Итерационный процесс продолжается до тех пор, пока все хi(k) не станут достаточно близкими к хi(k-1). Критерий близости можно задать в виде:
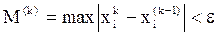 ,
,
где определяется максимальное значения разности для всех i, а e – некоторое положительное число. При выполнении критерия итерационный процесс следует остановить.
Обратимся к вопросу сходимости метода. Перед обобщением на случай n уравнений рассмотрим более простой пример – систему из 2-х уравнений. При этом возьмем систему, в которой диагональные коэффициенты по абсолютному значению будут больше недиагональных.
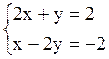 (2.9)
(2.9)
Точное решение системы:
х = 2/5, у = 6/5.
Из (2.9) запишем:
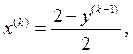

Результаты последовательных итераций составляют:
| Итерация | х | у |
| 3/2 | ||
| 1/4 | 9/8 | |
| 7/16 | 39/32 |
Графическое решение системы представлено на рисунке точкой пересечения двух прямых.

Рисунок 1.5 – Итерационный процесс решения системы (2.9)
Из таблицы видно, что итерационный процесс приводит нас к решению, которое с каждой итерацией приближается к точному решению системы, то есть итерационный процесс сходится.






