Процедура вычисления собственных значений и собственных векторов (собственных подпространств) линейного оператора 
вытекает из соответствующего теоретическоо материала. Продемонстрируем ее на конкретном примере.
Задача 3.4. Найдите собственные значения и собственные подпространства оператора 
(необходимо самостоятельно проверить линейность)
.
Решение. 1) Строим матрицу оператора 
в стандартном базисе 
пространства 
(предполагаем, что линейность оператора проверена):
, 
.
2) Составляем характеристическую матрицу 
, вычисляем ее определитель и находим корни характеристического многочлена.
;
;
Оба корня принадлежат полю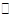 
и являются собственными значениями оператора; 
- кратности 1; 
- кратности 2.
3) Составляем систему линейных однородных уравнений с матрицей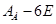 
и находим ее фундаментальную систему решений:
Система ранга 2. Множество ее решений - одномерное пространство, линейно независимых решений. Легко находим ее фундаментальную систему решений - 
. Собственное подпространство, относящееся к
4) Составляем систему линейных однородных уравнений с матрицей 
и находим ее фундаментальную систему решений:
Система ранга 2. Множество ее решений также является одномерным пространством. Легко находим ФСР - 
. Собственное подпространство, относящееся к
Задача решена.
Замечание 1. Если оператор задан своей матрицей, то пункт 1) не нужен.
Замечание 2. Если в процессе решения получилась несовместная система, то допущена ошибка (неверно вычислен характеристический многочлен, найденное 
не является собственным значением или допущена ошибка в вычислении коэффициентов системы линейных уравнений или в процессе решения системы).
Замечание 3. Полезно помнить, что размерность собственного подпространства, относящегося к собственному значению у любого линейного оператора не превышает (меньше или равна) кратности этого собственного значения, как корня характеристического многочлена (геометрическая кратность собственного значения его алгебраической кратности). Например, в задачах №№1465, 1466, 1481 есть собственные значения с алгебраической кратностью 3, а их геометрическая кратность соответственно равна 1,2 и 3.
Замечание 4. В учебных примерах, как правило, корни характеристического многочлена вычисляются точно. На практике часто приходится довольствоваться их приближениями. Возникающие при этом проблемы достаточно сложны и здесь не обсуждаются.
