Пусть 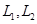 - данные подпространства пространства. Обычно их задают в виде линейных оболочек систем векторов или как множества решений некоторых однородных систем линейных уравнений, а сами векторы- координатными строками в некотором базисе. Вычисление
- данные подпространства пространства. Обычно их задают в виде линейных оболочек систем векторов или как множества решений некоторых однородных систем линейных уравнений, а сами векторы- координатными строками в некотором базисе. Вычисление 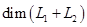 не составляет особого труда: это ранг объединения базисов или порождающих систем подпространств
не составляет особого труда: это ранг объединения базисов или порождающих систем подпространств  и
и  .
. 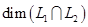 находится по формуле
находится по формуле
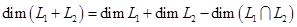 . (3)
. (3)
Несколько сложнее обстоит дело с поиском базиса пересечения 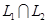 . В общем виде этот вопрос рассматривается в задаче №1319 [4]. Здесь же мы укажем, как найти решения конкретных задач (№№ 1320-1322 [4]). Задачу 1.6 мы решим двумя способами, второй - с помощью схемы Штифеля (предполагаем, что №1319 вы уже разобрали).
. В общем виде этот вопрос рассматривается в задаче №1319 [4]. Здесь же мы укажем, как найти решения конкретных задач (№№ 1320-1322 [4]). Задачу 1.6 мы решим двумя способами, второй - с помощью схемы Штифеля (предполагаем, что №1319 вы уже разобрали).
Задача 1.6. Найти базис суммы и пересечения подпространств, натянутых на системы векторов
 и
и 
Решение. Обозначим 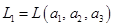 ,
, 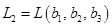 . Будем считать, что координаты векторов заданы в единичном базисе
. Будем считать, что координаты векторов заданы в единичном базисе  .
.
1 способ. Как известно, базисом суммы служит любая база системы векторов 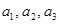 ,
,  . Его построение сводится к вычислению ранга матрицы, строками которой являются координаты векторов последней системы. Кроме того, базис суммы можно получить, добавляя к базису первого подпространства некоторые из векторов базиса второго подпространства.
. Его построение сводится к вычислению ранга матрицы, строками которой являются координаты векторов последней системы. Кроме того, базис суммы можно получить, добавляя к базису первого подпространства некоторые из векторов базиса второго подпространства.
Итак, 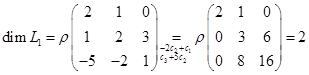 . Базис
. Базис  составляют
составляют 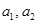 .
.
 . Базис
. Базис  составляют
составляют 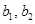 .
.
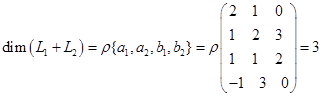 .
.
Базис 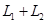 составляют
составляют 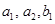 . По формуле (3) получаем
. По формуле (3) получаем  . Базис пересечения будем искать из условия
. Базис пересечения будем искать из условия 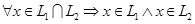 . Значит,
. Значит,  представим в виде
представим в виде  и
и 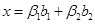 . Приравниваем правые части
. Приравниваем правые части 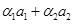
 . Это равенство эквивалентно системе трех линейных однородных уравнений с четырьмя неизвестными. Нужно решить эту систему и построить ФСР. Тогда
. Это равенство эквивалентно системе трех линейных однородных уравнений с четырьмя неизвестными. Нужно решить эту систему и построить ФСР. Тогда 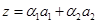
 будет образовывать базис пересечения.
будет образовывать базис пересечения.
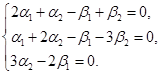
Решив систему, строим ФСР.

Вектор 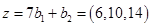 образует базис
образует базис 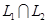 .
.
2 способ. 1) Составим таблицу Штифеля для объединенной системы векторов 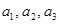 ,
, 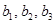 и перебрасываем наверх сначала векторы
и перебрасываем наверх сначала векторы  , пока это возможно (квадратиками выделены разрешающие элементы). Векторы
, пока это возможно (квадратиками выделены разрешающие элементы). Векторы 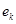 , переходящие налево, не пишем и их координаты не вычисляем.
, переходящие налево, не пишем и их координаты не вычисляем.
| а) | 
| 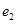
| 
| б) | 
| 
| 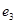
| ||

| 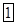
| 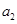
| -3 | ||||||
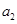
| 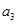
| -1 | -2 | 
| |||||
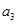
| -5 | -2 | 
| 
| -1 | 
| |||

| 
| -7 | |||||||
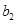
| -1 | 
| |||||||
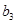
|
| в) | 
| 
| 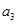
|
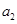
| |||

| 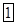
| ||
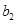
| -7 | ||
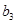
|
Перебросить 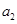 наверх вместо
наверх вместо  невозможно. Следовательно,
невозможно. Следовательно, 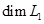 =2, а базис
=2, а базис  составляют
составляют  ,
, 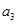 . Исключаем из таблицы строку
. Исключаем из таблицы строку 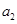 и перебрасываем наверх
и перебрасываем наверх 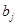 вместо оставшихся
вместо оставшихся 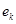 .
.
| г) | 
| 
| 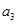
|
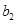
| -7 | 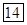
| |
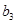
| -19 | -7 |
Из таблицы г) получаем: 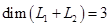 , то есть
, то есть 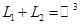 и базис суммы образуют векторы
и базис суммы образуют векторы  ,
,  ,
, 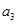 .
.
2) Продолжаем работу с таблицей г), перебрасывая наверх 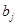 вместо находящихся наверху
вместо находящихся наверху  , пока это возможно. Как и выше, векторы, уходящие налево, опускаем.
, пока это возможно. Как и выше, векторы, уходящие налево, опускаем.
| д) | 
| 
| 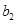
|
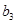
| -7 |
Вектор 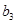 перебросить наверх вместо
перебросить наверх вместо  невозможно. Приходим к выводу, что
невозможно. Приходим к выводу, что 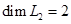 , базис
, базис  составляют
составляют  ,
, 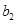 . По (3)
. По (3)  .
.
3) Возвращаемся к таблице г). Вектор 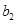 , вошедший в базис
, вошедший в базис  , представим через базис суммы
, представим через базис суммы 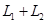 в виде:
в виде:
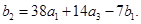
Отсюда находим 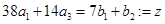 .
.
Вектор  и
и  , а так как
, а так как 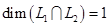 , то
, то  образует базис пересечения
образует базис пересечения 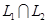 . Оба представления вектора
. Оба представления вектора  дают один результат
дают один результат  , что подтверждает правильность вычислений. Задача решена.
, что подтверждает правильность вычислений. Задача решена.
Для более полного усвоения понятия суммы, прямой суммы подпространств полезно решить задачи №№1323-1329 [4].
Задача 1.7. Для подпространства  , натянутого на векторы
, натянутого на векторы  , найти дополнительное подпространство.
, найти дополнительное подпространство.
Решение. Для любого подпространства  линейного пространства
линейного пространства  всегда найдется дополнительное подпространство
всегда найдется дополнительное подпространство  , то есть такое подпространство, что
, то есть такое подпространство, что  . Причем, оно определяется неоднозначно. Найдем одно из таких подпространств. Для этого мы должны найти базис
. Причем, оно определяется неоднозначно. Найдем одно из таких подпространств. Для этого мы должны найти базис 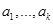 подпространства
подпространства  и дополнить его до базиса всего пространства
и дополнить его до базиса всего пространства  . Пусть
. Пусть 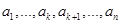 - базис
- базис  . Тогда
. Тогда  .
.
Найдем базис и размерность  .
.
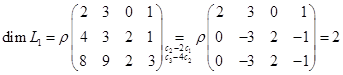 .
.
Базис  -
- 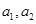 . Так как
. Так как  - сумма прямая, то
- сумма прямая, то 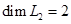 . Чтобы найти базис
. Чтобы найти базис  дополним базис
дополним базис  до базиса всего пространства
до базиса всего пространства 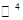 векторами
векторами 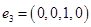 ,
, 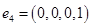 .
.
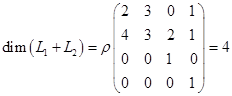 . Итак,
. Итак, 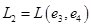 .
.






