Построение базиса пространства, подпространства несколько упрощается, если мы располагаем некоторыми представлениями о размерности пространства, подпространства. Одним из наводящих соображений здесь может быть следующее. Подмножество 
векторов пространства 
выделяется из с помощью дополнительных условий, накладываемых на векторы. При этом, чем больше таких условий, тем меньшей, вообще говоря, будет размерность подпространства . Если 
, а выделено с помощью 
условий специального вида, то есть основания ожидать, что 
.
Задача 1.1. (№1297[4]) Доказать, что множество п -мерных векторов, у которых первая и последняя координаты равны между собой, образует линейное подпространство пространства 
.
Решение. Множество образует линейное подпространство пространства , так как удовлетворяет критерию подпространства. Действительно, выделяется из с помощью одного условия 
, поэтому
1. 
,
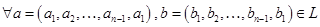
2. 
.
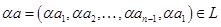Кроме того, нетрудно показать, что 
. Для этого рассмотрим векторы стандартного базиса 
. Векторы 
не принадлежат . Но построение базиса подпространства в ряде случаев удобно выполнить, исходя из стандартного базиса самого пространства, изменяя его векторы так, чтобы они «попали» в подпространство. Поэтому преобразуем векторы так, чтобы у них первая и последняя координаты были равны. Например, пусть 
. Рассмотрим систему векторов 
. Она образует базис , так как нетрудно проверить, что она является линейно независимой и каждый вектор из подпространства линейно выражается через вектора этой системы. А так как количество векторов системы равно 
, то и . Итак, наше предположение оказалось верным.
Линейные подпространства, размерности которых на 1 меньше размерности самого пространства называются гиперплоскостями.
В следующей задаче условий больше.
Задача 1.2. (№1298[4]) Доказать, что множество п -мерных векторов, у которых координаты с четными номерами равны нулю, образует линейное подпространство пространства .
Решение. Для доказательства того, что является подпространством, нужно также воспользоваться критерием подпространства. Так как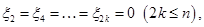 
поэтому следует ожидать, что 
, где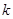 
- наибольшее четное число, не превышающее 
(
, если - четное, и 
, если - нечетное). Базисом является подсистема стандартного базиса пространства , содержащая векторы только с нечетными номерами.
Задача 1.3. Проверить, является ли множество многочленов степени 3 с вещественными коэффициентами подпространством пространства многочленов степени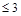 
(
).
Решение. Воспользуемся критерием подпространства. Проверим условие 
.
Пусть 
, тогда
,
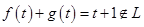так как степень суммы этих двух многочленов равна двум. Итак, множество не является подпространством.
Задача 1.4. (№№1291, 1308[4]) Найти какой-нибудь базис и размерность линейного подпространства пространства , если составляют все векторы из , у которых сумма координат 
.
Решение. Очевидно векторы стандартного базиса
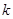(1 на - ой позиции) множеству не принадлежат ни при каком 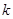. Однако, замена на векторах 
последнего нуля числом (-1) дает нам векторы из . Таким образом мы получаем систему векторов
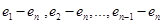
из , которая линейно независима (почему?) и обязана быть базисом , ибо из условия задачи явно следует, что из 
и, следовательно, 
.
Попутно решен вопрос (и подтвердилась гипотеза) о размерности (
выделено из одним условием).
Задача 1.4. (№1306[4]) Пусть 
- неотрицательная квадратичная форма от неизвестных ранга . Доказать, что все решения уравнения 
=0 образуют 
мерное линейное подпространство пространства .
Поиск решения. Вспоминаем основные понятия теории квадратичных форм (матрица формы, ранг формы, определение формы). Очевидно, что более подробные записи данного уравнения в виде 
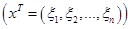, никак не указывают на способ решения задачи.
В процессе дальнейших размышлений начинаем понимать, что мы должны исходить из неотрицательной определенности формы . Нормальный вид такой формы
(1)
а множество решений уравнения =0 в этом случае состоит из векторов вида
, (2)
Где 
- произвольные числа из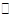 
. Имеющийся опыт (задача 1.2) подсказывает, что множество векторов такого вида есть (
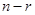)-мерное подпространство пространства . Но данная нам форма не обязательно нормальная. И здесь мы вспоминаем, что каждая неотрицательно определенная форма ранга невырожденным линейным преобразованием приводится к виду (1). Создается план решения: преобразовать форму к виду (1), найти решения (2) уравнения =0 для преобразованной формы, а затем с помощью обратного преобразования построить решения уравнения =0 для данной формы .
Решение. По теореме о приведении квадратичной формы к нормальному виду существует невырожденное линейное преобразование
, приводящее форму к виду
Множество решений уравнения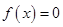 
состоит из векторов 
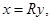где 
, то есть из векторов
.
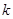Обозначим (1 на - ой позиции) и докажем, что множество решений уравнения 
=0 есть линейная оболочка системы векторов 
.
Пусть 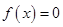. Тогда
Очевидно и другое:
Кроме того, система линейно независима (проверяется непосредственно). Составляем линейную комбинацию 
. Получаем 
. Мы пришли к матричному уравнению, которое имеет единственное решение, так как матрица 
является невырожденной.
.
Отсюда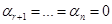 
. Тем самым мы показали, что система является линейно независимой. Следовательно, - линейное пространство (по построению) и его размерность 
