При расчете на прочность по допускаемым напряжениям исходными будут формулы, вытекающие из (5.11) и (6.5):
 max=
max= 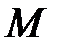 max
max 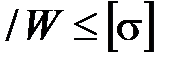 , (7.1)
, (7.1)
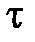 max=
max= 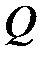 max
max 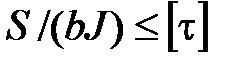 , (7.2)
, (7.2)
где 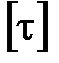 - допускаемое касательное напряжение.
- допускаемое касательное напряжение.
Для простоты будем считать, что материал балки одинаково сопротивляется растяжению и сжатию, а ее поперечное сечение симметрично относительно нейтральной оси.
Расчет по нормальным напряжениям в задачах изгиба является основным и первичным.
При этом, как и для ЦРС различают: проектный расчет, который заключается в подборе сечения по формуле, вытекающей из (7.1):
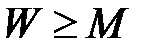 max/
max/ 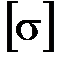 , (7.3)
, (7.3)
проверочный расчет прочности балки по формуле (7.1) и расчет несущей способности по формуле:
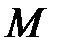 max
max 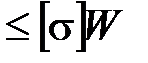 .
.
Расчет по касательным напряжениям также можно проводить в трех вариантах: как проектный, проверочный или в виде определения эксплуатационной нагрузки. Однако чаще всего приходится выполнять проверочный расчет - заданной балки или сечения, подобранного из условия прочности по предельным напряжениям.
При этом величина допускаемых касательных напряжений 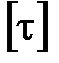 составляет порядка 0,1
составляет порядка 0,1 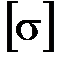 для деревянных балок и около 0,6
для деревянных балок и около 0,6 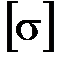 - для стальных.
- для стальных.
Отметим, что толщина стенок прокатных двутавровых балок, применяемых в строительстве, обычно удовлетворяет условию (7.2).
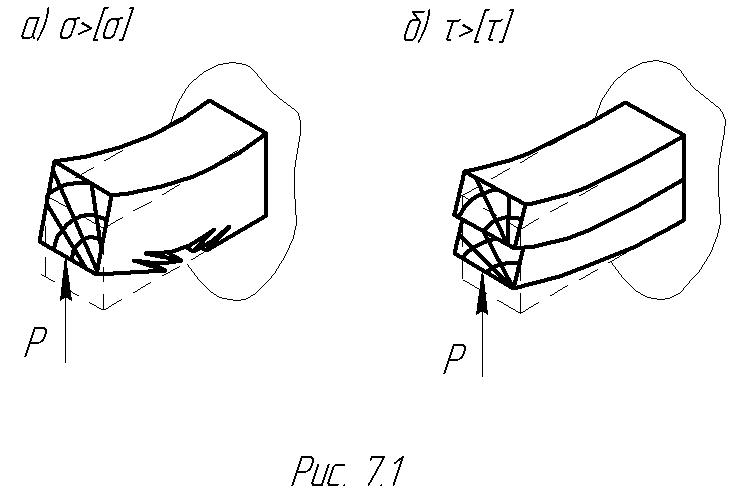
В отличие от них деревянные балки нужно обязательно проверять на прочность по касательным напряжениям, поскольку они имеют склонность к разрушению за счет скалывания, т.е. взаимного сдвига ее горизонтальных слоев (рис.7.1б). Мы уже выяснили в параграфе 6.1, что это сопровождается резким уменьшением жесткости сечения и, следовательно, приводит к нарушению условия прочности уже по нормальным напряжениям (рис.7.1а).
Пример 7.1. Подобрать сечение консольной балки длиной l = 2м, которая загружена равномерно распределенной нагрузкой интенсивностью 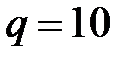 кН/м (см. рис.3.4), в двух вариантах: 1) прокатная двутавровая балка,
кН/м (см. рис.3.4), в двух вариантах: 1) прокатная двутавровая балка, 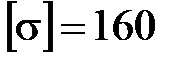 МПа,
МПа, 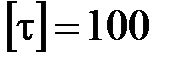 МПа; 2) деревянная балка квадратного поперечного сечения,
МПа; 2) деревянная балка квадратного поперечного сечения, 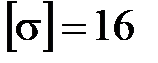 МПа,
МПа, 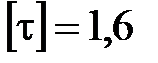 МПа.
МПа.
Решение. Максимальные значения изгибающего момента и поперечной силы для данной балки равны:
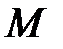 max=
max= 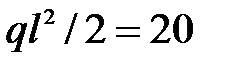 кН×м;
кН×м; 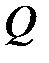 max=
max= 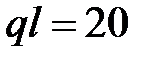 кН.
кН.
Для стальной балки размеры поперечного сечения находим из условия прочности по нормальным напряжениям (7.3):
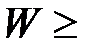
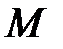 max
max 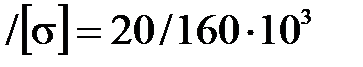 ×м3=
×м3= 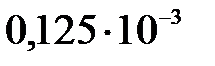 м3=125 см3.
м3=125 см3.
В сортаменте материалов этому условию отвечает двутавр №18 со следующими характеристиками сечения: 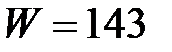 см3;
см3; 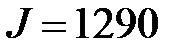 см4; статический момент полусечения
см4; статический момент полусечения 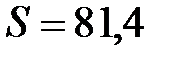 см3; толщина стенки
см3; толщина стенки 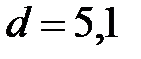 мм.
мм.
Максимальные касательные напряжения в таком двутавре по формуле (7.2) будут равны:
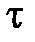 max=
max= 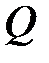 max
max 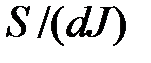 =
= 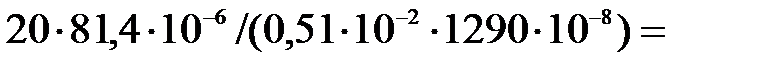 2,475×104 кПа =
2,475×104 кПа =
= 24,75 МПа 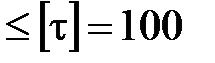 МПа,
МПа,
т.е. балка имеет четырехкратный запас прочности по касательным напряжением.
Для деревянной балки квадратного поперечного сечения со стороной 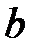 момент сопротивления
момент сопротивления 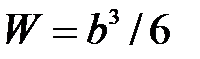 и условие (7.3) примет вид:
и условие (7.3) примет вид:
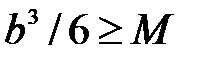 max
max 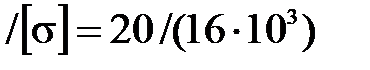 м3 = 1250 см3,
м3 = 1250 см3,
откуда 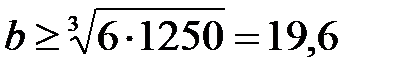 см.
см.
Округляя до ближайшего размера, рекомендованного в сортаменте пиломатериалов, принимаем 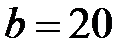 см.
см.
Статический момент полусечения такого бруса:
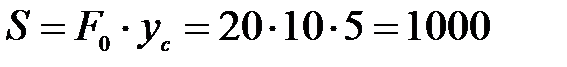 см3,
см3,
а момент его инерции:
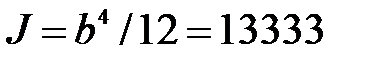 см4.
см4.
Подставляя в (7.2), получим:
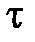 max=
max= 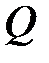 max
max 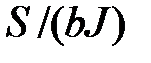 =
= 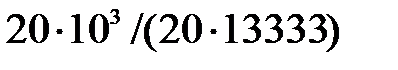 кН×см-2 =
кН×см-2 = 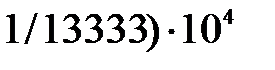 МН×м-2 =
МН×м-2 =
= 0,75 МПа 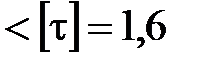 МПа,
МПа,
т.е. условие прочности выполняется. ·






