Предпосылки расчета
При поперечном изгибе в сечении стержня появляются не только нормальные напряжения s z, эквивалентные изгибающему моменту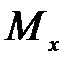 
:
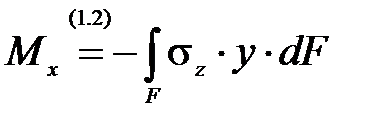, (6.1)
но и касательные напряжения t zy, эквивалентные поперечной силе Qy:
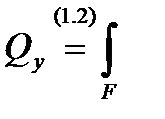t zy × dF. (6.2)
Подобно тому, как в предыдущей главе мы перешли от (6.1) к формуле (5.10), сейчас нам предстоит выразить t zy из (6.2) через поперечную силу Qy.
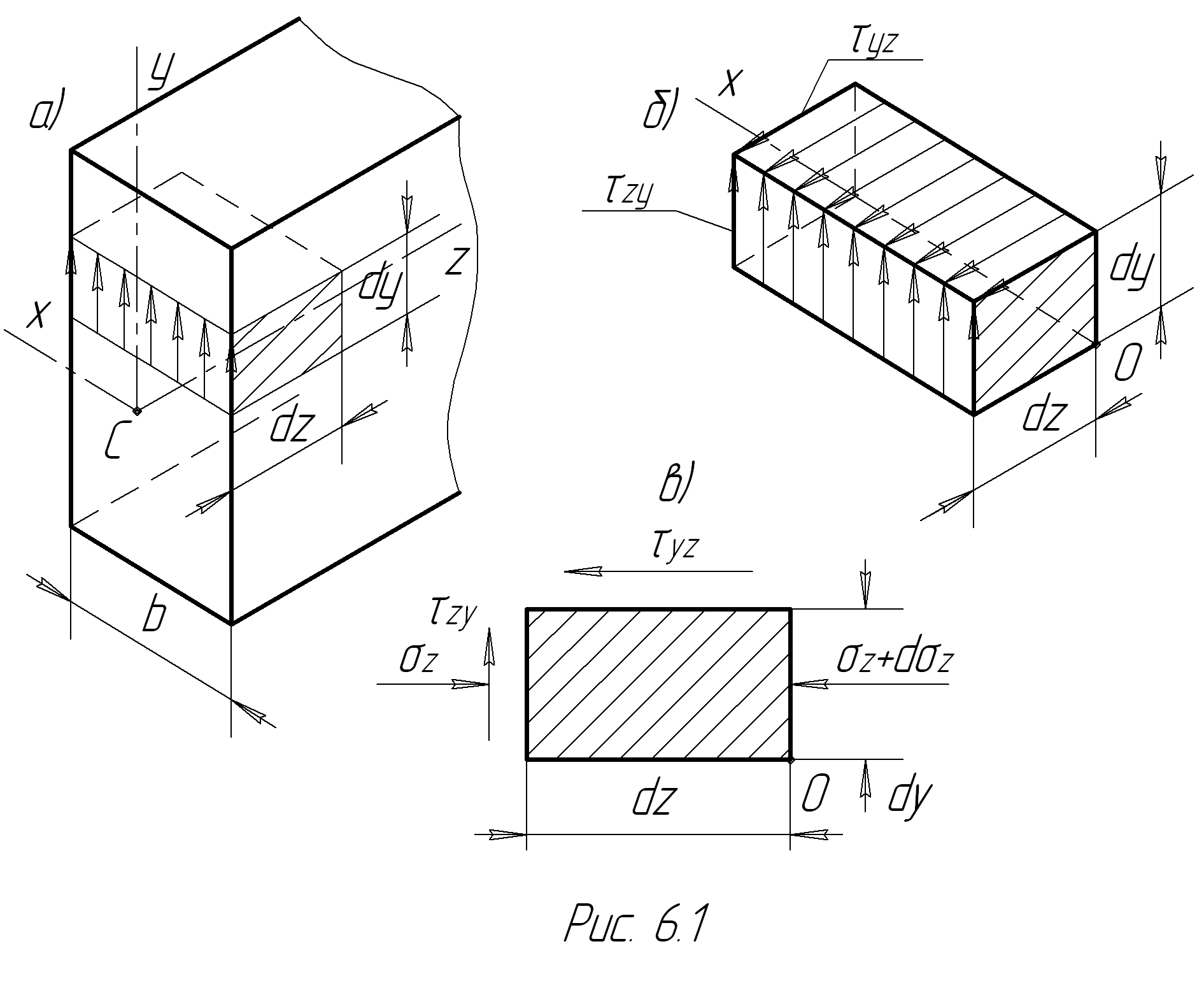
Рассмотрим часть балки шириной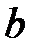 
, расположенную справа от сечения, и предположим, что касательные напряжения равномерно распределены поперек этого сечения (рис.6.1а).
Тогда из условий равновесия призматического элемента балки размерами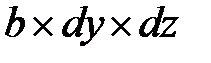 
следует, что касательные напряжения t zy, действующие по его передней грани, должны уравновешиваться напряжениями 
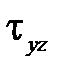в его верхней плоскости (рис.6.1б). При этом уравнение равновесия
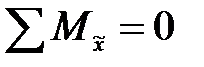, (6.3)
относительно оси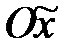 
, параллельной 
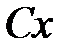, примет вид:
,
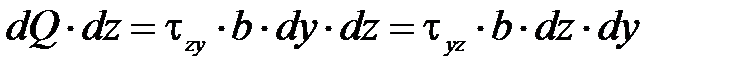откуда следует, что
= 
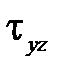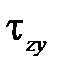. (6.4)
Аналогичные соотношения справедливы не только для балки, но и для любого упругого тела - они выражают закон парности касательных напряжений, в соответствии с которым касательные напряжения на смежных гранях прямоугольного параллелепипеда равны по модулю и направлены навстречу друг другу (см. рис.1.9).
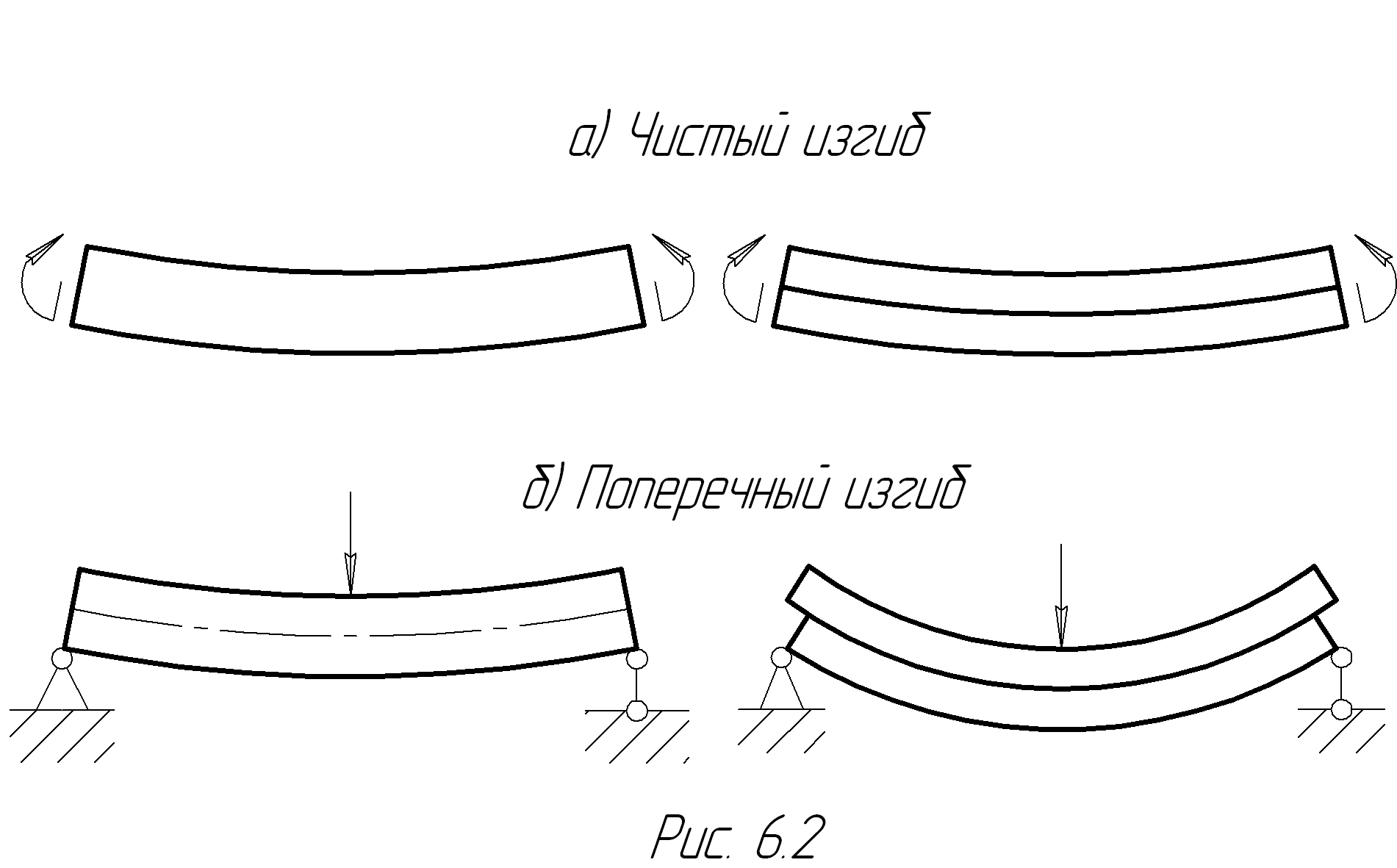
Итак, касательные напряжения появляются не только в поперечных сечениях балки, но и между ее горизонтальными слоями. Чтобы убедиться в этом, проведем мысленно следующий эксперимент. Рассмотрим две балки одинаковой длины: одна - в виде сплошного бруса, а другая - в виде того же бруса, распиленного вдоль на две части. При чистом изгибе разница в балках ничем не проявляет себя, и они деформируются совершенно одинаково (рис.6.2а). В случае поперечного изгиба значительно больше будут прогибы второй балки; ее слои свободно смещаются относительно друг друга в отличие от слоев первой балки, взаимно удерживаемых именно касательными напряжениями (рис.6.2б).
ПРИМЕЧАНИЯ:
1. Мы предполагаем, что касательные напряжения в поперечном сечении балки направлены параллельно поперечной силе Qy, то есть вдоль оси Oy.
2. Вполне оправданным будет вопрос: почему при выводе формулы (6.4) мы не учитывали нормальные напряжения?
В самом деле, при поперечном изгибе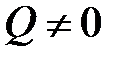 
, а 
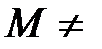const. Пусть в рассматриваемом сечении балки (рис.6.1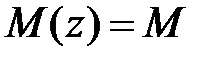а) 
, а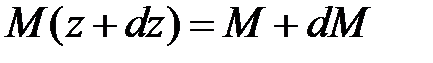 
. Тогда в силу (5.10) на переднюю грань вырезанного элемента помимо 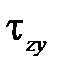будут действовать 
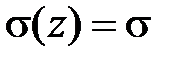, а на противоположную s(z + dz) = s + d s, знаки которых учтены на рис.6.1в. С учетом этих напряжений уравнение (6.3) примет вид:
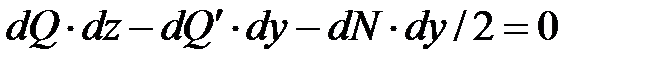
или, подробнее:
,
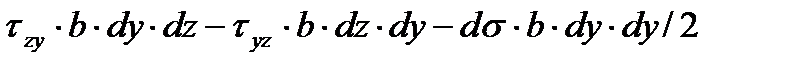откуда
(t zy - t yz) = (d s/ dz)×(dy /2).
Подставляя сюда
,
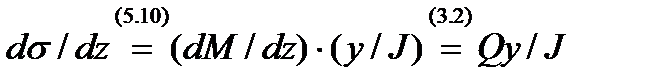получим соотношение:
.
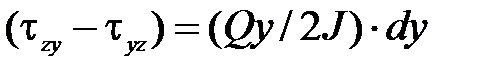С точностью до бесконечно малых первого порядка правая часть последнего выражения равна нулю, откуда и следует (6.4).
3. Нетрудно уточнить, насколько прогибы второй балки на рис.6.2б будут больше, чем у первой. Из условия равенства изгибающих моментов и уравнения (5.9) следует, что отношение кривизн обратно пропорциональны отношению жесткостей балок:
.
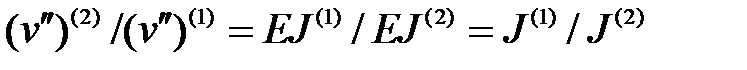Для балки прямоугольного поперечного сечения:
,
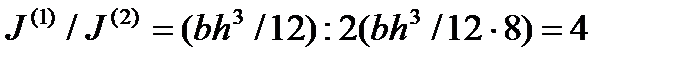а поскольку прогибы балки v = v (P, l, EJ), то с точностью до множителя v = Pl 3 / EJ, откуда следует, что прогибы второй балки будут вчетверо больше прогибов первой.
Формула Журавского
Появление касательных напряжений между горизонтальными слоями балки позволяет легко определить их величину.
Рассмотрим часть балки длиной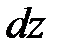 
, расположенную между двумя сечениями, проведенными на расстояни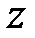и 
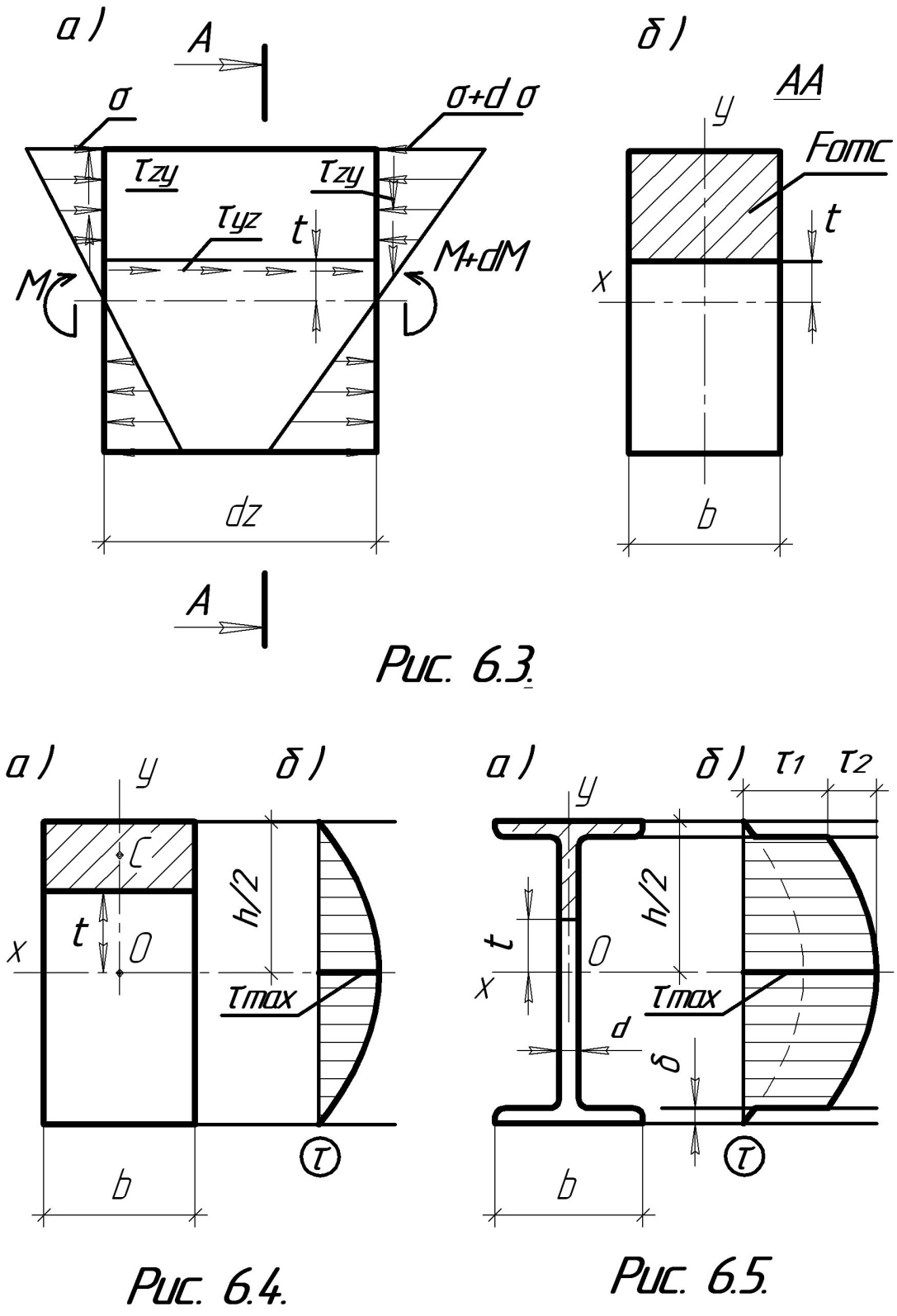
и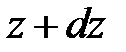 
от ее левого конца (рис.6.3а). Изгибающим моментам 
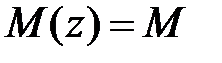и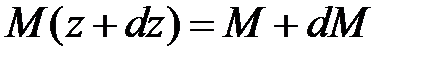 
в этих сечениях балки будут, в силу (5.10), соответствовать нормальные напряжения 
и s+ d s.
Проведем горизонтальное сечение на расстоянии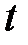 
от нейтральной оси и рассмотрим равновесие части балки выше этого сечения. Помимо нормальных и касательных напряжений, приложенных в сечениях 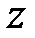и 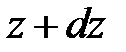, на нее будут действовать касательные напряжения 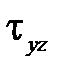, распределенные по площади нижней грани и уравнение 
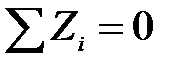примет вид:
,
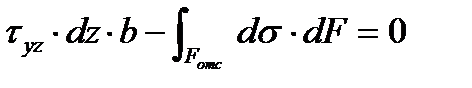где F отс - площадь части поперечного сечения балки выше рассматриваемого уровня (рис.6.3б).
Подставляя с учетом (5.10) в последнее выражение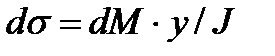 
, получим
,
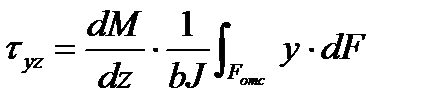или, с учетом (3.2) и (4.2):
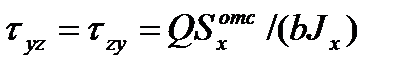, (6.5)
где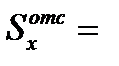 
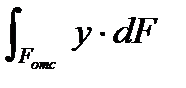- статический момент части сечения выше рассматриваемого уровня.
Последнее выражение и носит название формулы Д.И.Журавского.
ПРИМЕЧАНИЯ:
1. При выводе формулы (6.5) поперечное сечение балки фактически предполагается выпуклым и односвязным. То есть, эту формулу нельзя, например, формально применить к балке Т -, О - или П -образного поперечного сечения.
2. В этом курсе не рассматривается изгиб тонкостенных стержней открытого профиля, для которых не выполняется не только предпосылка о равномерном распределении касательных напряжений поперек сечения балки (параграф 6.1), но и гипотеза прямых нормалей (параграф 5.1).
