Критическое напряжение и гибкость стержня

Определение. Критическим напряжением σ_кр называется напряжение в стержне, вызванное силой P _кр:

 

σ_кр = P _кр/ F = (p² EJ _min)/ F (m l)² = (p² E )/(m l)²,

 

где = J _min/ F, а = – минимальный радиус инерции сечения стержня.

Обозначим, следуя Ф. Ясинскому, через λ = m l / i_min гибкость стержня – безразмерную величину, определяемую:

- длиной стержня и способом закрепления его концов,

- формой и размерами поперечного сечения.

Тогда видоизмененная формула Эйлера примет вид:

 

σ_кр =p² E /λ², (11.7)

 

то есть график зависимости σ_кр(λ) представляет собой гиперболу (рис. 11.8).

λпр

λ0

σпц

λ

σт

σкр = (p2 Е)/λ2

σкр

рис. 11.8

 

Формально из (11.7) следует, что σ_кр = ∞, однако вывод формулы Эйлера основан на применении дифференциального уравнения изогнутой оси стержня, материал которого следует закону Гука. Поэтому эта формула верна только при постоянном модуле упругости E, то есть при условии, что критическое напряжение σ_кр не превышает предела пропорциональности σ_пц.

Предельная гибкость стержня, отвечающая условию σ_кр = σ_пц в силу (11.7) будет равна:

λ_пр = p ,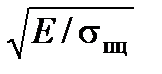

 

при этом λ_пр зависит только от механических свойств материала и является константой.

Приведем взятые из [11] значения гибкости стержня некоторых материалов:

- сталь Ст3 (σ_пц = 195 МПа, E = 206 ГПа), λ_пр = 3,14 = 102,

 

- древесина сосны (σ_пц = 20 МПа, E = 10 ГПа), λ_пр = 70.

 

Таким образом, формула Эйлера применима только к упругим стержням, и ее распространение на стержни, теряющие устойчивость за пределом упругости (σ_пц), неверно, поскольку приводит к завышенным значениям σ_кр и P _кр. Поэтому соответствующая часть графика σ_кр(λ), выделенная пунктиром, не реализуется.

При потере устойчивости за пределом упругости критические напряжения определяются по более сложным законам или по эмпирическим зависимостям, при этом реальная кривая σ_кр(λ) будет проходить между линиями 1 и 2 на этом графике. В простейшем варианте эту кривую можно аппроксимировать отрезком прямой, как это сделано в формуле Тетмайера – Ясинского:

 

σ_кр(λ) = a - b λ, (11.8)

 

где коэффициенты a и b определяются по экспериментальным данным.

При этом для стали Ст3 a = 305 МПа, b = 1,12 МПа; для древесины сосны a = 28,7 МПа, b = 0,19 МПа.

Полученные на основе (11.8) результаты также представляют интерес только до некоторого значения λ₀, при котором критические напряжения достигают опасных напряжений сжатия: пределу текучести σ_т – для пластичных или пределу прочности σ_пч – для хрупких материалов.

Для стали Ст3, например λ₀ =30 – 40, поэтому эта часть графика, соответствующая зависимости (11.8), также заменена отрезком σ_кр(λ) = σ_т.

Таким образом, сжатые стержни делятся на три категории:

- стержни большой гибкости (λ > λ_пр), для которых σ_кр находят по формуле Эйлера;

- стержни средней гибкости (λ₀ <λ< λ_пр), которые рассчитывают по формуле Тетмайера – Ясинского;

- стержни малой гибкости (λ< λ₀), для которых опасна потеря не устойчивости, а прочности – для них σ_кр = σ_т или σ_кр = σ_пч.