Для определения постоянных Е, 
и других характеристик материалов, необходимых для расчета, проводят механические испытания их стандартных образцов с заданной длиной l и площадью поперечного сечения F. В ходе такого испытания находят зависимость изменения длины образца D l от величины действующей силы N, а фактически – строят график 
как функции 
. С учетом особенностей этих диаграмм 
все материалы делятся на два класса:
1) пластичные (сталь, алюминий);
2) хрупкие (стекло, чугун).
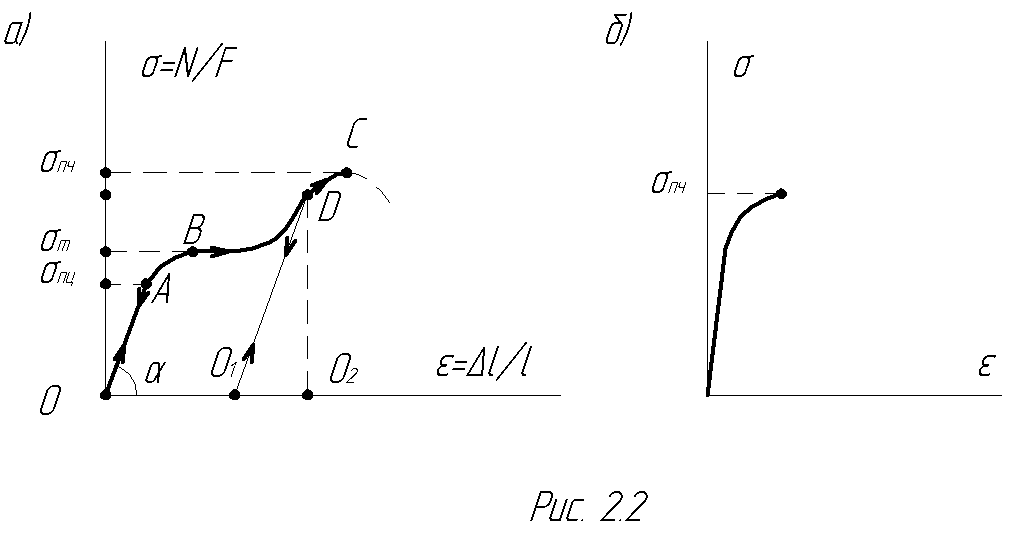
Рассмотрим диаграмму растяжения стального образца, на которой отмечены характерные точки и соответствующие им напряжения (рис.2.2а).
Пределом пропорциональности (sпц) называется максимальное напряжения, соответствующее точке А диаграммы, при котором сохраняется линейный характер зависимости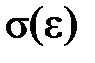 
в соответствии с законом Гука. Сравнивая уравнение прямой ОА: 
с (2.6), получим, что Е 
.
Пределом текучести (sт) называется напряжение, при котором деформирование образца происходит без увеличения нагрузки, что вызвано перестройкой структуры стали. Горизонтальный участок диаграммы в окрестности точки В называется площадкой текучести.
Предел прочности (sпч) – максимальное напряжение, которое выдерживает образец до разрушения.
Проследим теперь за образцом при уменьшении приложенной к нему нагрузки.
Если в процессе его загрузки напряжение не превысило sпц, то разгрузка происходит по той же прямой ОА, по которой происходило нагружение, и после снятия приложенной нагрузки тело полностью восстановит свои размеры и форму.
Разгрузка из точки D, принадлежащей участку АС, происходит по прямой О 1 D, параллельной ОА.
Таким образом, полная деформация стержня в точке D – ОО 2 складывается из упругой – О 1 О 2 и пластической или остаточной ОО 1.
Поведение хрупких материалов при растяжении характеризуется разрушением в упругой стадии при незначительных деформациях. На диаграмме растяжения таких материалов есть только одна характерная точка, соответствующая sпч (рис.2.2б).
Свойства хрупких материалов, в отличие от пластичных, при растяжении и сжатии различны, поэтому для них строят обе диаграммы. Такие материалы как бетон или кирпич испытывают только на сжатие, т.к. они практически не работают на растяжение.
ПРИМЕЧАНИЯ:
1. В действительности между точками А и В на диаграмме (рис.2.2а) расположена еще одна точка, которой соответствует напряжение предел упругости (sупр), близкое по значению к (sпц). В рамках этого курса мы будем считать sпц равным sупр.
2. Мы рассмотрели процесс испытания образца и определение свойств материала в самом первом приближении. В действительности характер диаграммы зависит от многих факторов, в том числе – скорости деформирования и температуры проведения испытаний, поэтому для ряда материалов правильнее говорить не об их принадлежности к тому или иному классу, а о проявлении у них соответствующих свойств в определенных условиях.
3. Приведенная диаграмма (рис.2.2а) носит условный характер, т.к. не учитывает изменение первоначальной длины стержня l и площади его поперечного сечения F в ходе испытания и, особенно, на его завершающей стадии. В рамках этого курса не рассматривается механизм разрушения деформируемого тела.
Расчет на прочность
Теория и практика расчета на прочность, появившись в позапрошлом веке, продолжают развиваться и совершенствоваться вместе с механикой деформируемого тела.
С учетом гипотез, рассмотренных в параграфе 1.4, отметим только два метода расчета на прочность:
– расчет по допускаемым напряжениям;
– расчет по предельным состояниям.
Первый из них давно известен, но продолжает оставаться актуальным. Его суть заключается в сравнении напряжений в конструкции от заданной нагрузки с их предельными значениями, получаемыми с учетом диаграммы нагружения. Для ЦРС соответствующее условие прочности имеет вид:
smax= N/F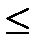 
[s], (2.7)
где smax – максимальное по модулю напряжение, N – продольная сила в опасном поперечном сечении, F – площадь этого сечения, [s] – допускаемое напряжение материала бруса.
Последнее определяется следующим образом: для пластичных материалов: [s] = sт /кт; для хрупких материалов: [s] = sпч /кпч, где кт, кпч - коэффициенты запаса прочности по отношению к пределу текучести и пределу прочности соответственно.
Эти коэффициенты создают запас прочности, который должен компенсировать возможное отрицательное влияние таких факторов, как:
– неточность выбора расчетной схемы;
– ошибки в определении величины действующей нагрузки и несоответствие условиям эксплуатации;
– неточность изготовления элементов конструкции;
– несоответствие физических характеристик материала конструкции паспортным данным и другие факторы.
Напомним, что расчет на прочность является необходимым этапом решения основной задачи СМ - проектирования конструкции. Такой проектный расчет заключается в подборе сечения по формуле, вытекающей из (2.7):
[s].
Помимо него может возникнуть необходимость проверочного расчета прочности эксплуатируемой конструкции, который выполняется непосредственно по формуле (2.7), или расчета несущей способности по следующей из нее формуле:
[s] F.
Основным недостатком метода допускаемых напряжений является то, что с помощью одного коэффициента запаса прочности одновременно учитывается несколько различных по своей природе факторов. Это приводит к трудностям при проектировании конструкций, которые одновременно должны быть надежными и экономичными.
Метод расчета по предельным состояниям, известный также как метод частных коэффициентов и введенный в практику проектирования строительных объектов во второй половине прошлого столетия, предусматривает, как и следует из его второго названия, введение отдельных коэффициентов надежности по нагрузке, материалу, назначению, а также коэффициентов условий работы и др.
ПРИМЕЧАНИЕ. К числу конструкций, находящихся в условиях ЦРС или элементы которых испытывают этот вид НДС, относятся стойки, колонны, опоры, фермы и др. Если такие стержни обладают достаточной гибкостью, то при сжатии они могут разрушиться из-за потери устойчивости при напряжении, значительно меньшем допускаемого напряжения [s].
ГЛАВА 3. ПРЯМОЙ ИЗГИБ 
Внутренние усилия в балке
Рассмотрим брус в системе координат Oxyz, где начало отсчета выбрано на его левом конце, а ось Оz совпадает с осью бруса, проходящей через центры тяжести его поперечных сечений. Загрузим брус моментами и силами, лежащими в плоскости его симметрии Oyz, причем все силы Pi будем считать перпендикулярными к его оси Oz (рис.3.1а). Изгиб при указанных предпосылках называется прямым.
В дальнейшем под балкой будем понимать брус в условиях прямого изгиба.
Рассмотрим поперечный изгиб такой балки. Для внутренних усилий в ее сечении (рис.3.1б) можно дать простое и удобное на практике определение, которое в отличие от приведенного в параграфе 1.6, не связано с системой координат.
Поперечная сила Qу=Q в сечении балки равна сумме проекций на нормаль к ее оси всех сил, взятых по одну сторону от сечения, которое делит балку на две части.
Изгибающий момент Мх=М в сечении балки равен сумме моментов всех сил, взятых по одну сторону от сечения и вычисленных относительно точки, где сечение пересекает ось балки.
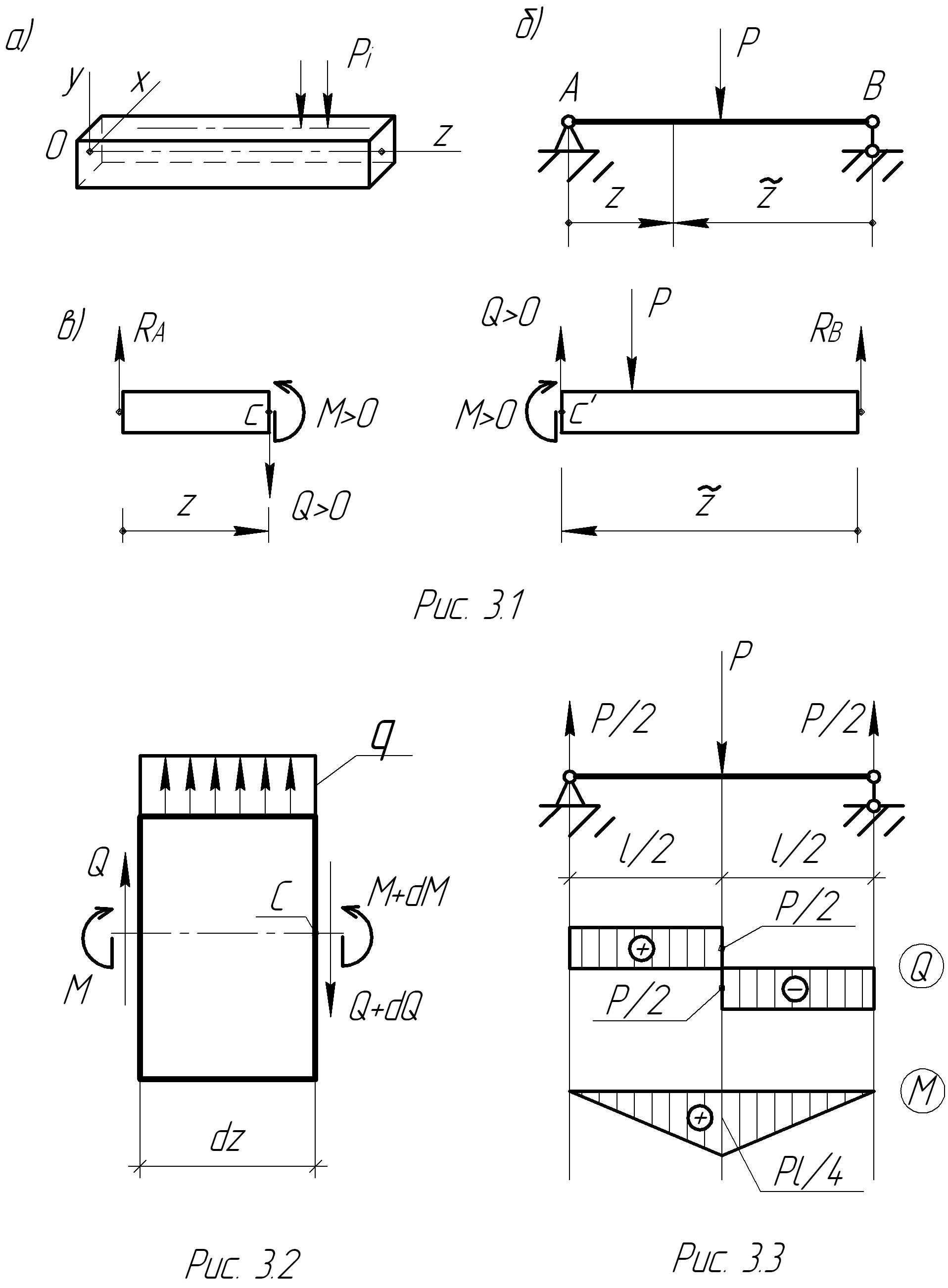
Правило знаков – в соответствии с рис.3.1в, где показаны положительные значения Q и M для частей балки, расположенных по обе стороны от проверенного сечения.
ПРИМЕЧАНИЯ:
1. Отметим, что Q > 0 соответствует вращению отсеченной части балки по ходу часовой стрелки.
2. Очевидно, что вычисление Q и M в сечении заданной двухопорной балки на расстоянии z от ее левого конца (рис.3.1б) не отличается от определения опорных реакций в консольной балке соответствующей длины. При этом последняя балка защемлена на правом конце и загружена всеми силами, взятыми слева от рассматриваемого сечения заданной балки. Аналогичное замечание справедливо для части балки справа от сечения (рис.3.1в).
3. В сечении, проведенном на расстоянии z от левого конца балки, Q = Q (z) и М = =М (z), причем абсциссы z и 
связаны зависимостью: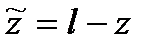 
.
Теорема Журавского
Рассмотрим участок балки длиной dz, заключенный между сечениями с абсциссами z и z + dz и загруженный распределенной нагрузкой с интенсивностью q (z). Слева на него действуют внутренние усилия Q (z)= Q и М (z)= M, справа – Q (z+dz)= Q+dQ и М (z+dz)= M+dM (рис.3.2).
Составим уравнения равновесия выделенного элемента, считая, что в его пределах распределенная нагрузка постоянна: q (z) = q.
Первое из уравнений:
; 
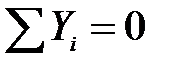приводит к соотношению:
| q = dQ / dz |
(3.1)
Из второго уравнения равновесия:
; 
,
пренебрегая бесконечно малыми второго порядка, получим еще одну зависимость:
| Q = dМ/dz |
(3.2)
Таким образом, функци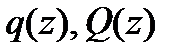и 
и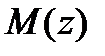 
связаны соотношениями (3.1) и (3.2), которые и составляют суть теоремы и называются дифференциальными зависимостями Журавского.
ПРИМЕЧАНИЕ. Для 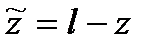эти зависимости примут вид: 
и 
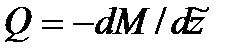соответственно.
3.3. Построение эпюр Q и M
Под эпюрой в СМ понимают график изучаемой величины, ординаты которого откладывают в направлении нормали к оси эпюры.
Последняя может совпадать с осью стержня, быть параллельной ей, либо представлять собой иную линию, полученную пересечением связанных с конструкцией поверхностей и плоскостей. При этом у арки или криволинейного стержня ось эпюры также может быть криволинейной – в отличие от оси Ох при построении обычных графиков функций.
Эпюры Q и М позволяют наглядно представить наиболее напряженные участки балки. Рассмотрим, например, эти эпюры для простой двухопорной балки (рис.3.3). Нетрудно догадаться, что опасным будет сечение в середине балки, где М (z) принимает максимальное значение.
При построении эпюр Q и М целесообразно придерживаться определенной последовательности.
Порядок построения эпюр Q и М
1. Определяем опорные реакции.
2. Делим балку на участки, границами которых являются:
- начало и конец балки,
- точки приложения сосредоточенных сил Рi и моментов Mi,
- границы участков распределенной нагрузки.
3. В пределах каждого участка балки проводим сечение на расстоянии zi от левого, или 
– от правого конца. Вычисляем Q и М как функции zi или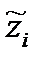 
, рассматривая условия равновесия соответствующей части балки слева или справа от сечения.
4. Строим эпюру Q, откладывая положительные значения вверх от оси эпюры, т.е. в направлении оси Оу и – эпюру М, откладывая положительные значения вниз от оси эпюры, т.е. на нижних волокнах балки.
5. Контроль правильности решения.
Остановимся подробнее на этом последнем и самом важном этапе решения.
