Из формул (3.1) и (3.2) следует:
1. На незагруженных участках балки (q = 0) эпюра Q – постоянна, а М – линейна.
2. На участках, загруженных равномерно распределенной нагрузкой (q = = const), – а мы будем рассматривать только такую, – эпюра Q представляет собой прямую линию, а М – параболу, обращенную выпуклостью в сторону действия нагрузки (правило «парусности эпюры»).
3. В точках приложения сосредоточенных сил Рi эпюра Q имеет скачок на величину приложенной силы, а эпюра М – точку излома в сторону действия силы.
В точках приложения сосредоточенных моментов Мi эпюра М имеет скачок на величину приложенного момента. (На эпюре Q это никак не отражается).
В частности, на концах балки значения Q и М будут равны соответственно – сосредоточенным силам и моментам, приложенным там (активным или реактивным).
4. На участке, где эпюра М нисходящая (возрастает), – Q > 0, если эпюра М – восходящая, – Q < 0.
5. Изгибающий момент может достигать максимального по модулю значения:
- на границах участков;
- в точках, где Q = 0;
- в точках приложения сосредоточенных сил, где эпюра Q имеет скачок со сменой знака.
ПРИМЕЧАНИЯ:
1. Для вычисления Q и М в каком-либо сечении балки удобнее рассматривать равновесие той части балки, к которой приложено меньше сил. Например, при построении эпюр, приведенных на рис.3.3, на первом участке ( ) из условия равновесия левой части (рис.3.1б, в) получим:
) из условия равновесия левой части (рис.3.1б, в) получим:
 ;
;  ;
;
 - RA × z + M (z) = 0; M (z) = Pz /2.
- RA × z + M (z) = 0; M (z) = Pz /2.
Тот же результат можно получить, рассматривая на этом участке  равновесие части балки, которая расположена справа от сечения:
равновесие части балки, которая расположена справа от сечения:
 ;
;  ;
;
 ;
; 
 .
.
2. На границе участков функции Q (z) и М (z) могут иметь точки разрыва. Например, в рассмотренном примере (рис.3.3), значения Q (z) слева и справа от сечения z = l /2 соответственно равны:  и
и  . Вопрос о том, чему равняется эта функция непосредственно в точке z = l /2, не имеет практического значения. Поэтому в качестве характерных точек, где вычисляются необходимые для построения эпюр значения функции, на каждом участке можно брать его границы, добавляя к ним – в случае распределенной нагрузки – точку в середине участка или точку, где Q = 0.
. Вопрос о том, чему равняется эта функция непосредственно в точке z = l /2, не имеет практического значения. Поэтому в качестве характерных точек, где вычисляются необходимые для построения эпюр значения функции, на каждом участке можно брать его границы, добавляя к ним – в случае распределенной нагрузки – точку в середине участка или точку, где Q = 0.
3. При построении эпюр в консольных балках можно не определять опорные реакции, если рассматривать равновесие части балки, не содержащей опору.
4. При рассмотренном правиле построения эпюры М она будет расположена на растянутых волокнах балки.
Примеры построения эпюр
Переходя к рассмотрению примеров, отметим, что, помимо изложенного выше метода построения эпюр, существуют и другие методы, однако разница между ними невелика и все они базируются на приведенном в параграфе 3.1 определении Q и М. Поэтому при решении этих задач надо помнить о следующем:
- значения Q и М в любом сечении балки можно вычислить просто в соответствии с этим определением;
- верное решение в общем случае можно получить только при условии правильного определения опорных реакций, для которых рекомендуется указывать их истинное направление;
- заключительным и самым важным этапом решения задачи является контроль правильности построения эпюр, рассмотренный в параграфе 3.3.
Во многих случаях решение задач можно упростить, если воспользоваться рассмотренным в параграфе 1.4 принципом суперпозиции, в соответствии с которым эпюры Q и М от заданной нагрузки можно найти как суммы соответствующих эпюр от каждой нагрузки в отдельности. При реализации этого метода полезно знать решения для простых двухопорных и консольных балок, загруженных сосредоточенными силами, моментами и распределенной нагрузкой - подобных рассмотренным на рис. 3.3.
Пример 3.1. Построить эпюры Q и М (рис.3.4а).
Решение. Балка состоит только из одного участка, границы которого совпадают с ее естественными границами.
Опорные реакции можно не определять, если рассматривать равновесие части балки, расположенной справа от сечения, проведенного на расстоянии 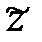 от ее свободного правого конца (рис.3.4б):
от ее свободного правого конца (рис.3.4б):
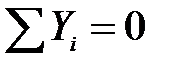 ;
; 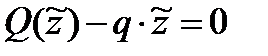 ;
;  ; (а)
; (а)
 ;
;  ;
;  . (б)
. (б)
 Строим эпюры Q и М по зависимостям (а) и (б), контролируя правильность решения задачи:
Строим эпюры Q и М по зависимостям (а) и (б), контролируя правильность решения задачи:
– на загруженном участке балки  – парабола,
– парабола,  – линейная функция;
– линейная функция;
– зависимости Журавского принимают вид:
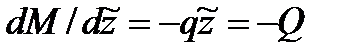 ;
; 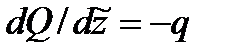 ;
;
– нисходящая (слева - направо!) эпюра М соответствует положительным значениям Q;
– на левом конце балки эпюры Q и М имеют скачки на величину соответственно опорной реакции RA = ql и реактивного момента МA = ql 2/2, где знаки последних соответствуют правилу ТМ (рис.3.4).
Отметим, что
МА ТМ = ql 2/2, МА СМ =– ql 2/2. ·
Как видим, опорные реакции можно найти не только из уравнений равновесия балки, но и с помощью построенных эпюр.
Пример 3.2. Построить эпюры Q и М (рис.3.5а).
Решение. В соответствии с планом, приведенным в параграфе 3.3:
1) Находим опорные реакции из условий равновесия балки (рис.3.5б):
å МА = 0;  = 0; RB = 1,5 кН;
= 0; RB = 1,5 кН;
å МВ = 0; –RA  ; RA = 2,5 кН.
; RA = 2,5 кН.
Проверка:
å Y = RA –  + RB = 2, 5 –
+ RB = 2, 5 – 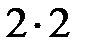 +1, 5 = 0.
+1, 5 = 0.
2) Делим балку на участки:
– первый участок:  ;
;
– второй участок:  (или
(или  ).
).
3) Определяем Q и М, рассматривая равновесие части балки слева от сечения – на первом и справа от сечения – на втором участке (рис.3.5в).

3.1) Первый участок
 ; RA –
; RA – 
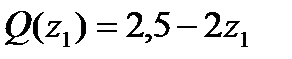 ; (а)
; (а)
 ; –RAz 1+
; –RAz 1+  ;
;  . (б)
. (б)
Для построения Q вычисляем ее значения на границе участка:
 . (в)
. (в)
Поскольку функция  меняет знак, находим корень уравнения
меняет знак, находим корень уравнения  :
:  .
.
Для построения эпюры  , представляющей собой параболу, вычисляем ее значения в трех точках:
, представляющей собой параболу, вычисляем ее значения в трех точках:
 ;
;  ;
;  . (г)
. (г)
3.2) Второй участок
 ;
;  RB =0;
RB =0;  RB =
RB =  (д)
(д)
 ;
;  + RB
+ RB  = 0;
= 0;  ; (е)
; (е)
 ;
;  . (ж)
. (ж)
4) Строим эпюры Q и М по вычисленным значениям (в), (г) и (ж).
5) Проверяем правильность построения эпюр:
– зависимости Журавского на первом участке – из (а) и (б):
 ;
;
– то же на втором участке – из (д) и (е):
 ;
;
– нисходящему участку эпюры М ( ) соответствует
) соответствует  ;
;
– эпюра Q на концах балки имеет скачки на величину RA и RB соответственно, у эпюры М - скачок в точке приложения сосредоточенного момента.
Отметим, что максимальное значение изгибающего момента: М max = = max(1,56; 3) = 3кНм достигается на границе участка. ·
Пример 3.3. Построить эпюры Q и М методом суперпозиции(рис.3.6а).
Решение. Суть этого метода – в том, чтобы вместо одной сложной задачи решить три (в данном примере), но простых.
На трех участках из четырех эпюра М от заданной нагрузки будет линейной, поэтому ограничимся построением только этой эпюры. Будем искать ее в виде суммы:  , где слагаемые представляют собой эпюры моментов от загружения заданной балки соответственно –
, где слагаемые представляют собой эпюры моментов от загружения заданной балки соответственно –  и М,и для их построения можно воспользоваться полученными ранее решениями.
и М,и для их построения можно воспользоваться полученными ранее решениями.
Эпюра Mq на первом участке заданной балки:  симметрична эпюре, приведенной на рис. 3.4, причем Mq (2) = – ql 2/2 = – 2кНм. На последнем участке (
симметрична эпюре, приведенной на рис. 3.4, причем Mq (2) = – ql 2/2 = – 2кНм. На последнем участке ( ) по определению
) по определению  , а на незагруженном участке между опорами А и В она изменяется по линейному закону.
, а на незагруженном участке между опорами А и В она изменяется по линейному закону.
Аналогично, не определяя опорных реакций, можно построить эпюру Mp на основе эпюры, приведенной на рис.3.3. Эпюра  строится аналогично
строится аналогично  .
.

Теперь для построения М достаточно вычислить ее значение в точке  : M (4) = Mq (4) + Mp (4) + MM (4) = - 1 + 4 + 1 = 4кНм (рис.3.6б).
: M (4) = Mq (4) + Mp (4) + MM (4) = - 1 + 4 + 1 = 4кНм (рис.3.6б).
Переходим к построению эпюры Q.
На первом участке она обратносимметрична эпюре, приведенной на рис.3.4. На незагруженных участках балки эпюру Q легко построить по эпюре М, воспользовавшись зависимостью 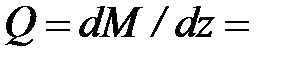 tga:
tga:
– на втором участке 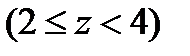 :
:
 tga1= (4+2)/2=3 кН;
tga1= (4+2)/2=3 кН;
– на третьем  :
:
 – tga2= – (4 – 2)/2= – 1 кН;
– tga2= – (4 – 2)/2= – 1 кН;
– на последнем четвертом участке  М = const, поэтому Q = 0 (рис.3.6в).
М = const, поэтому Q = 0 (рис.3.6в).
По эпюре Q находим реакции опор (рис.3.6г) и выполняем статическую проверку правильности решения:
 RA –P + RB =
RA –P + RB =  . ·
. ·






