Напомним, что НДС бруса определяется 6-ю компонентами: Qx, Qy, Nz, Mx, My, Mz.
Ранее были рассмотрены следующие виды НДС:
1) ЦРС (Nz ≠ 0),
2) Чистый изгиб (Mx ≠ 0 или My ≠ 0),
3) Поперечный изгиб (Mx ≠ 0, Qy ≠ 0 или My ≠ 0, Qx ≠ 0),
4) Сдвиг (Qx ≠ 0 или Qy ≠ 0).
Определение. НДС бруса называется сложным, если одновременно два или более компонент отличны от нуля. Исключение составляет поперечный изгиб, относящийся к простым видам НДС.
Косой изгиб
Этот вид НДС рассматривается как альтернатива прямому изгибу бруса (см. §3.1). Напомним, что изгиб бруса называется прямым, если выполнены два условия:
- силовая плоскость совпадает с плоскостью симметрии бруса,
- силы, приложенные к брусу перпендикулярны оси бруса.
Рассмотрим брус прямоугольного поперечного сечения длиной l в системе координат Oxyz, где начало отсчета выбрано на его левом защемленном конце, а ось Оz совпадает с осью бруса.
Пусть свободный конец бруса загружен силой Р, лежащей в плоскости поперечного сечения и направленной под углом α к оси Oy (рис. 10.1).
Очевидно, что в этом случае силовая плоскость не совпадает с плоскостью симметрии бруса, то есть не выполняется первое условие.
Составляющая силы Р по оси Oy вызывает изгиб бруса в вертикальной плоскости – относительно оси Ox – с максимальным изгибающим моментом Mx = Р cosα· l = М cosα, а сила Рх = Р sinα – изгиб в горизонтальной плоскости (относительно оси Oy) с максимальным изгибающим моментом My = Р sinα· l = = М sinα.
Таким образом, косой изгиб эквивалентен двум прямым изгибам во взаимно перпендикулярных плоскостях. При этом
σ = σ(Mx) + σ(My) = (Mx / Jx) y + (My / Jy) x = M [(cosα/ Jx) y +(sinα/ Jy) x ]. (10.1)
Чтобы построить эпюру результирующих напряжений, определим положение нейтральной оси. Подставляя в (10.1) σ = 0 и учитывая, что M ≠ 0, получим:
y = - (sinα/ Jy)/(cosα/ Jx) x = - tgα (Jx/Jy) x,
и обозначив
tgβ = tgα (Jx/Jy), (10.2)
получим искомое уравнение нейтральной оси:
y = - tgβ x. (10.3)
| у |
| Рх |
| Рис. 10.1 |
| α |
| Ру |
| РО |
| О |
| х |
| z |
Как видим, она проходит через центр тяжести сечения и лежит во втором и четвертом квадрантах.
Отметим, что если Jx ≠ Jy, то и β ≠ α, то есть нейтральная ось не перпендикулярна силовой плоскости.
Дальнейший ход построения эпюры результирующих напряжений не требует комментариев (рис. 10.2).
Расчет балки на прочность при косом изгибе выполняют по формуле, аналогичной формуле (7.1) для прямого изгиба:
 |max = (Mx / Wx) + (My / Wy) ≤ [
|max = (Mx / Wx) + (My / Wy) ≤ [ 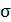 ].
].
Максимальные прогибы консоли от сил Рy = Р cosα и Рх = Р sinα найдем с помощью универсального уравнения изогнутой оси балки (см. пример 8.3):
fx = (Рхl 3)/(3 EJy); fy = (Рyl 3)/(3 EJx).
Тангенс угла между плоскостью симметрии бруса Oyz и плоскостью прогибов равен:
tgγ = (fx / fy) = tgα (Jx/Jy) = tgβ,
то есть плоскость прогибов перпендикулярна нейтральной оси бруса.
| силовая плоскость |
| нейтральная ось |
| γ |
| у |
| х |
| Р |
| +σ(Му) |
| σ(Мх) |
| α |
| Рис. 10.2 |
| + |
| - |
| β |
| + |
| - |
| σmax |
| плоскость прогибов |
Прямой изгиб с ЦРС
Пусть теперь не выполняется второе условие прямого изгиба, о котором шла речь в начале §10.1, и свободный конец бруса загружен силой Р, приложенной в центре тяжести сечения, которая лежит в плоскости симметрии бруса, но не перпендикулярна его оси (рис. 10.3).
Разложим силу Р на составляющие по осям Oy и Oz. Тогда сила Рz будет вызывать растяжение бруса с постоянной продольной силой Nz = Рz и постоянными нормальными напряжениями σ(N) = N / F, а сила Рy – изгиб в вертикальной плоскости с максимальным изгибающим моментом Mx = Рy · l, и нормальными напряжениями σ(Mx) = (Mx / Jx) y.
| у |
| Рz |
| Рис. 10.3 |
| α |
| Ру |
| РО |
| О |
| х |
| z |
Результирующие нормальные напряжения будут равны:
σ = σ(N) + σ(Mx) = N / F + (Mx / Jx) y.
Таким образом, при изгибе с растяжением нейтральная ось не проходит через центр тяжести сечения (рис. 10.4).
При этом
σmax = N / F + Mx / Wx;
σmin = N / F - Mx / Wx.
Эти формулы справедливы и для случая сжимающей продольной силы, но только при условии, что балка имеет большую изгибную жесткость, когда соблюдается принцип начальных размеров.
Условие прочности:
 |max = N / F + Mx / Wx ≤ [
|max = N / F + Mx / Wx ≤ [ 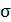 ].
].
| Рис. 10.4 |
| σ(Mx) |
| σ(N) |
| х |
| у |
| σmax |
| О |
| + |
| + |
| + |
| σmin |
| - |
| нейтральная ось |






