Моменты инерции относительно параллельных осей

Для определения геометрических характеристик сложных сечений, составленных из стандартных прокатных профилей (двутавр, швеллер и др.), нужно знать соотношения между моментами инерции этих элементов относительно собственных центральных осей, приведенными в сортаменте, и моментами инерции относительно центральных осей всего сечения.

Рассмотрим две системы координат и (рис.4.1), связанные зависимостями:

; .

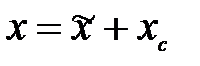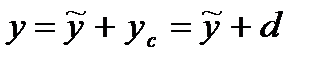Для момента инерции из (4.4) с учетом последнего соотношения получим:

 

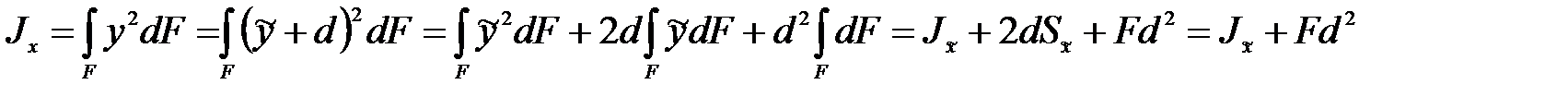,т.к. (см. параграф 4.1).

Таким образом, момент инерции сечения относительно какой-либо оси равен моменту инерции относительно параллельной ей центральной оси плюс площадь сечения, умноженная на квадрат расстояния между осями:

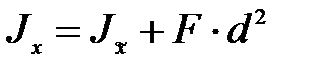
. (4.6)

 

Моменты инерции простых сечений

 

К числу наиболее распространенных форм поперечных сечений балок, особенно деревянных, относятся прямоугольник и круг.

Прямоугольник. Рассмотрим поперечное сечение балки шириной b и высотой h и определим его момент инерции (4.4) относительно оси (рис.4.2).

Разобьем площадь сечения F на полоски шириной h и высотой и положим 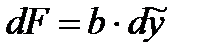. Тогда интегрирование по площади F сведется к вычислению одномерного интеграла:

.

 

Итак, момент инерции прямоугольника:

(4.7)

Круг. Определим вначале момент инерции круга радиуса R относительно его центра О (рис.4.3). Проще всего вычислить соответствующий интеграл в (4.4), разбивая круг на кольца шириной dr и полагая dF равной площади этого кольца.

 

С точностью до бесконечно малых первого порядка , поэтому:

Теперь с помощью (4.5) легко найти и :

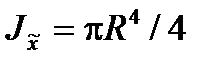
(4.8)

 

Пример 4.1. Вычислить центральный момент инерции балки треугольного поперечного сечения (рис.4.4а).

Решение. Рассмотрим сечение в виде квадрата со стороной (рис.4.4б). Полагая в (4.7) , найдем момент инерции квадратного сечения относительно оси .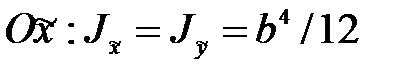

Воспользовавшись для квадрата соотношением (4.5), получим:

 

,

откуда .

_

Из (4.4) следует, что момент инерции составного сечения относительно какой-либо оси равен сумме моментов инерции отдельных частей этого сечения относительно той же оси. Поэтому, представив квадрат на рис.4.4б в виде двух треугольников, разделенных осью , получим, что момент инерции каждого из них относительно оси будет равен:

.

Возвращаясь к рис.4.4а, найдем для заданной балки:

 

.

 

Центр тяжести треугольника отстоит от центра О на расстояние 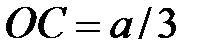, поэтому расстояние между осями 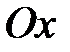и равно .

Воспользовавшись зависимостью 4.6, получим:

. ·

ГЛАВА 5. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ

Предпосылки расчета

Мы выяснили, что напряжения в поперечном сечении балки статически эквиваленты внутренним усилиям, которые находят из условий равновесия ее отсеченной части. Однако, для расчета на прочность недостаточно определить М и Q - нужно знать именно напряжения и 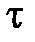. Чтобы выразить последние через внутренние усилия (1.2), надо ввести дополнительные гипотезы, отражающие особенности деформирования балки и распределение напряжений по площади ее сечения, - подобные введенной при рассмотрении ЦРС.

Для обоснования соответствующих предпосылок рассмотрим балку прямоугольного поперечного сечения в условиях чистого изгиба с нанесенной на ее боковой поверхности ортогональной сеткой (рис.5.1).

 

Как видим, ее нижние волокна - растягиваются, верхние - сжимаются, а образующие нейтральный слой - остаются недеформированными. При этом размеры сечения по оси не меняются, а сами сечения остаются перпендикулярными к изогнутой оси балки.

Это позволяет ввести в рассмотрение две гипотезы.

1. Статическая гипотеза. Горизонтальные слои балки не давят друг на друга, т.е. .

2. Кинематическая гипотеза. Сечения, перпендикулярные к оси балки до деформации, остаются перпендикулярными к ее изогнутой оси. При этом перемещения точек нейтрального слоя балки вдоль осей и равны нулю.

Как показывает опыт, применение этих гипотез оправдано и в случае поперечного изгиба балки.

Определение. Прямая, полученная пересечением нейтрального слоя с плоскостью поперечного сечения, называется его нейтральной осью.

 

ПРИМЕЧАНИЯ:

1. Кинематическая гипотеза, известная как гипотеза плоских сечений Я.Бернулли, фактически применялась нами еще в параграфе 2.1 при рассмотрении деформации ЦРС: введенная там предпосылка о постоянстве в поперечном сечении стержня с учетом закона Гука (2.6) означала постоянство , а в силу (2.4) - также и w.

2. Рассмотренные гипотезы, особенно в случае поперечного изгиба, соответствуют действительности только приближенно:

- вблизи мест приложения нагрузки нарушается статическая гипотеза о несдавливании горизонтальных слоев;

- первоначально плоские поперечные сечения при деформации могут искривляться и так далее.

Тем не менее, полученные на их основе результаты расчета вполне отвечают потребностям инженерной практики.

 

Перемещения и деформации

Рассмотрим балку в системе координат 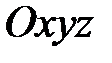, где ось балки совпадает с осью , проходящей через нейтральные оси сечений (рис.5.2а).

z

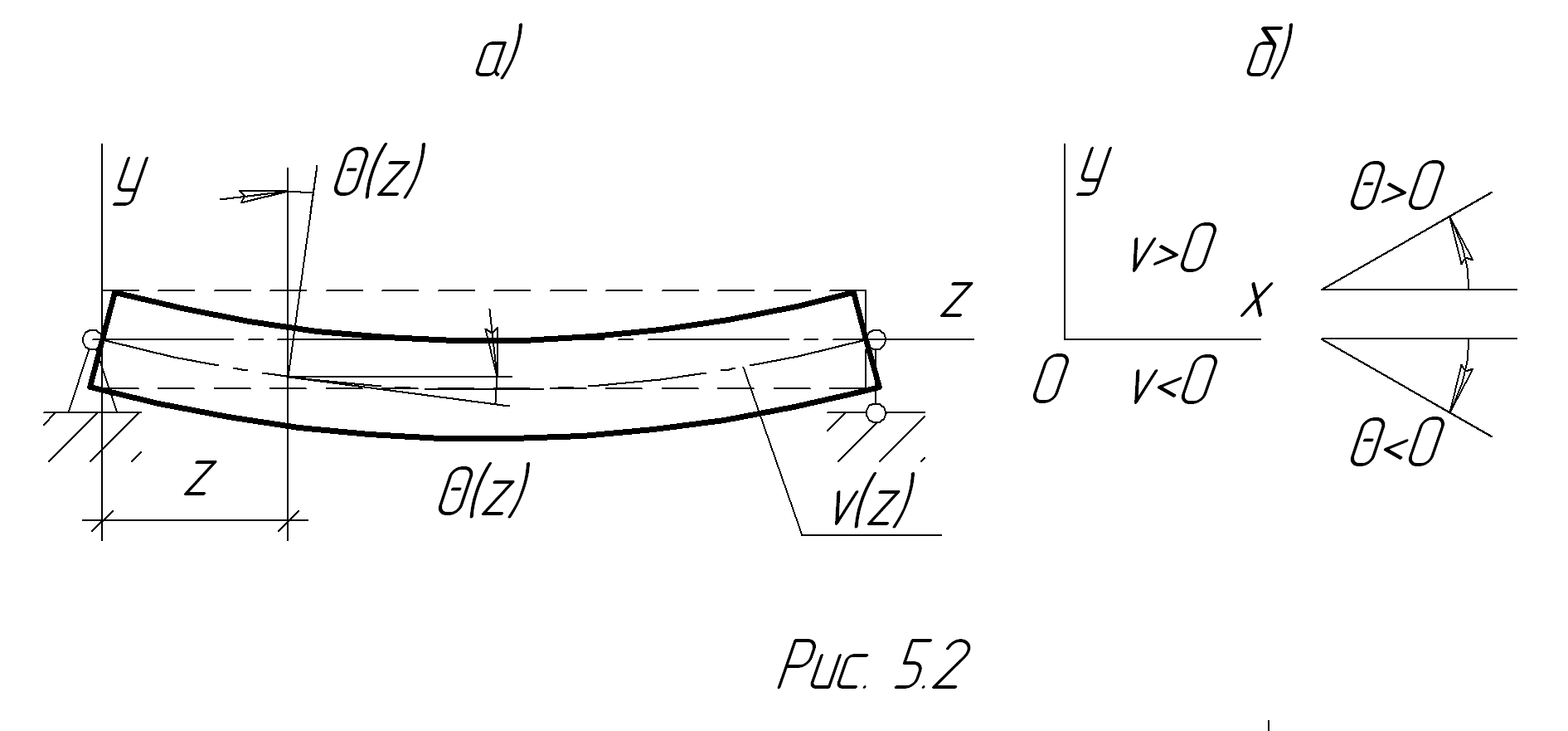
Прогибами балки называются перемещения точек ее оси, которые с учетом кинематической гипотезы возможны только в направлении оси .

Изогнутой осью балки называется кривая , которую принимает ось балки при деформации.

Угол поворота сечения равен углу наклона касательной к изогнутой оси балки. На основании гипотезы малости перемещений (параграф 1.4):

 

θ(z) ≈ sin θ ≈ tg θ = dv / dz. (5.1)

Правило знаков - в соответствии с рис.5.2б.

Отметим, что в силу гипотезы Бернулли перемещения всех точек балки описываются перемещениями точек, лежащих в плоскости ее симметрии Oyz.

Чтобы проследить за точками балки, не лежащими на ее оси, рассмотрим консоль длиной z, защемленную на левом конце и загруженную на правом - моментом (рис.5.3).

Зафиксируем на свободном конце балки точку А - пусть она находится на расстоянии у от нейтральной оси, проходящей через точку С, и в результате деформации занимает в пространстве положение .

Из найдем модуль проекции вектора перемещения на ось Оz: | w (z)| = A ¢ B = A ¢ C ¢sin q = y sin q.Принимаяво внимание (5.1) и заменяя приближенное равенство строгим, получим с учетом знака w (z):

w (z) = - y tg q = - y dw / dz. (5.2)

В силу статической гипотезы отдельные слои балки ведут себя как при ЦРС, поэтому деформации можно найти по формуле (2.3):

e _z . (5.3)

Таким образом введенные в предыдущем параграфе гипотезы, позволяют выразить перемещения и деформации точек балки через уравнение ее изогнутой оси .

ПРИМЕЧАНИЯ:

1. Фактически изменение длины волокна балки, проходящего через точку А ее сечения, равно не отрезку , а отрезку A ¢ B ¢ = y tgq, и (5.1) означает, что (рис.5.3б).

2. Для строгого обоснования формулы (5.3) нужно рассмотреть, как это было сделано в параграфе 2.1, часть балки длиной , где - радиус кривизны изогнутой оси балки и найти непосредственно по формуле (2.2):

 

e _z . (5.4)

Переход от (5.4) к (5.3) означает, что в выражении кривизны:

(5.5)

 

мы пренебрегаем членом 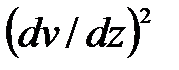, величина которого, в соответствии с действующими в строительстве нормами, не превышает 10^-4.

 

Нормальные напряжения

Рассмотрим балку произвольного симметричного сечения в системе координат 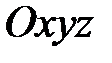, где ось совпадает с нейтральной осью, а Oy - является осью симметрии сечения.

Мы уже говорили, что отдельные слои балки фактически находятся в условиях ЦРС, поэтому напряжения в них, с учетом закона Гука, можно найти по формуле (2.6):

. (5.6)

Таким образом, напряжения пропорциональны удалению точек сечения от его нейтральной оси (рис.5.4).

К сожалению, на практике мы не можем воспользоваться последней формулой по двум причинам:

- неизвестно положение нейтральной оси ;

- мы не знаем, чему равно значение .

Для ответа на эти вопросы, воспользуемся выражениями внутренних усилий через напряжения (1.2), а также учтем формулы (5.6) и (4.2):

 

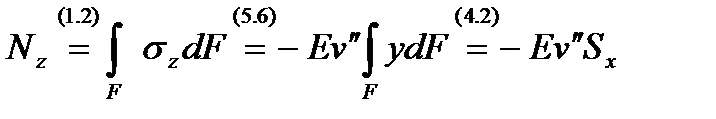; (5.7)

. (5.8)

Поскольку при изгибе балки 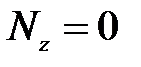, то из (5.7) следует, что , т.е. нейтральная ось проходит через центр тяжести сечения.

Изгибающий момент в балке отличен от нуля и, как следует из (5.8), пропорционален изгибной жесткости балки :

.

(5.9)

 

Поделив (5.6) на (5.9), получим искомое выражение для нормальных напряжений s = s _z в поперечных сечениях балки:

.

(5.10)

 

Как видим, максимальные по модулю напряжения будут в точках сечения, наиболее удаленных от его нейтральной оси:

 

max , (5.11)

где

max (5.12)

- момент сопротивления сечения. Это основная геометрическая характеристика прочности балки.

Для прямоугольного сечения (рис.4.2) max = , поэтому .