Рассмотрим множество балок, имеющих одинаковые по величине максимальные изгибающие моменты М. Пусть поперечные сечения этих балок равны по площади - F, но различны по форме. Естественно возникает вопрос: какая форма поперечного сечения будет наилучшей?
Для ответа на него нужно, прежде всего, формулировать критерий оптимальности. С учетом условия прочности при ЦРС (2.7):
smax= 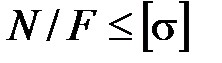
наилучшей можно считать балку, у которой максимальные по модулю нормальные напряжения минимальны:
max  min. (5.13)
min. (5.13)
В силу (5.11) последнее выражение при фиксированном значении М примет вид:
 max, (5.14)
max, (5.14)
т.е. из множества балок с одинаковой площадью поперечного сечения оптимальной будет балка с наибольшим значением момента сопротивления W.
Последний вывод, конечно, требует пояснения, и для этого мы рассмотрим следующий пример.
Предположим, в нашем распоряжении - стальная балка квадратного поперечного сечения со стороной  см (рис.5.5а). Площадь и момент сопротивления такого сечения будут, соответственно, равны:
см (рис.5.5а). Площадь и момент сопротивления такого сечения будут, соответственно, равны: 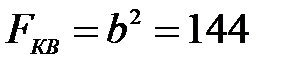 см2;
см2;  см3.
см3.
Качество балки можно заметно улучшить, если, пропустив через прокатный стан, превратить ее в балку прямоугольного поперечного сечения шириной  см и высотой
см и высотой  см (рис.5.5б). Соответствующие параметры такой балки будут равны:
см (рис.5.5б). Соответствующие параметры такой балки будут равны: 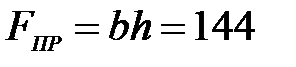 см2;
см2;  см3.
см3.
Продолжив мысленно наш эксперимент, можно из имеющегося образца изготовить балку двутаврового поперечного сечения высотой  см с толщиной стенки
см с толщиной стенки 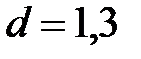 см (рис.5.5в). Для соответствующей стандартной балки несколько меньшей площади поперечного сечения
см (рис.5.5в). Для соответствующей стандартной балки несколько меньшей площади поперечного сечения 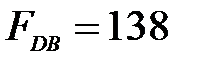 см2 с толщиной стенки
см2 с толщиной стенки  см, момент сопротивления
см, момент сопротивления  см3.
см3.

Таким образом,  , т.е. последняя балка в 6 раз прочнее прямоугольной и в 9 раз прочнее балки квадратного поперечного сечения.
, т.е. последняя балка в 6 раз прочнее прямоугольной и в 9 раз прочнее балки квадратного поперечного сечения.
Можно ли продолжить этот процесс поиска более совершенной и прочной балки при заданной площади поперечного сечения? Или, другими словами, ограничено ли максимальное значение W?
Как теория, так и практика дают положительный ответ на последний вопрос. Попытка создать двутавровую балку с большим моментом сопротивления за счет увеличения высоты и соответствующего уменьшения толщины ее стенки не приведет к созданию более прочной балки. Причина этого - в том, что с уменьшением толщины стенки балки увеличивается опасность потери ее устойчивости. Это явление сопровождается выпучиванием стенки балки и имеет ту же природу, что и рассмотренная ранее (рис.1.4а) потеря устойчивости сжатого стержня. Отметим, что при этом двутавровая балка перестает отвечать критерию стержневых систем (параграф 1.2) и переходит в разряд тонкостенных пространственных конструкций.




