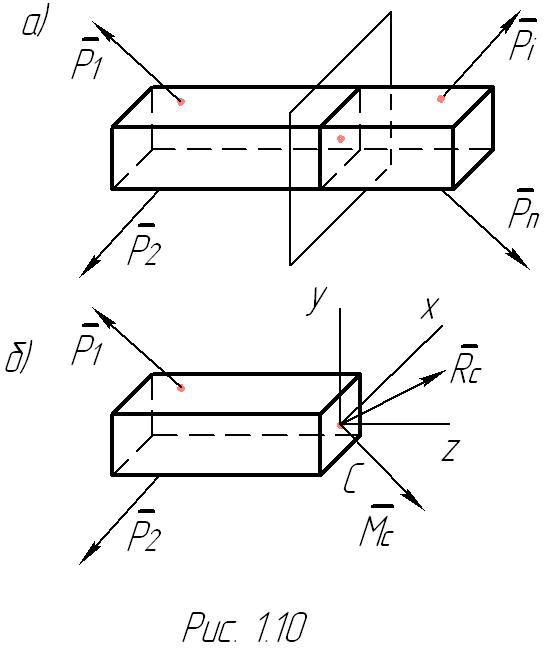
Применим рассмотренный в предыдущем параграфе метод сечений к частному случаю тела - брусу, загруженному уравновешенной системой сил (рис. 1.10а). Проведем сечение и рассмотрим равновесие части стержня слева от сечения под действием сил Р 1, Р 2 и реакций отброшенной правой части или
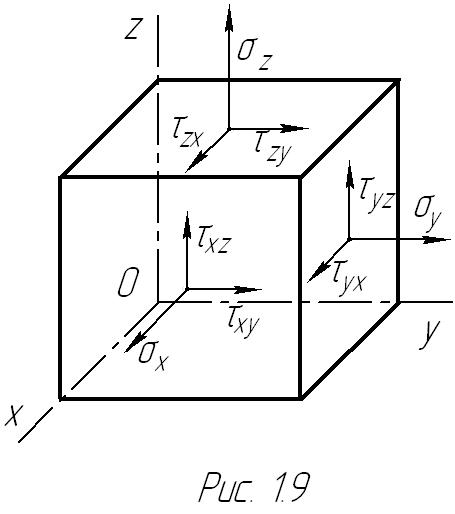напряжений. Приведем последние к центру, выбрав в качестве него точку C - центр тяжести сечения.
Введем систему координат с началом в центре C и обозначим через Rc и Mc главный вектор и главный момент реакций отброшенной правой части (рис. 1.10б).
Определение. Внутренними усилиями в стержне называются проекции векторов Rc и Mc на оси координат системы Cxyz, взятые с определенным знаком.
Условие равновесия отсеченной части:
(Р 1, Р 2, Rс, Mc) ~ 0
эквивалентно уравнениям равновесия:
å C = 0; å U = 0; å Z = 0; å Mx = 0; å My = 0; å Mz = 0,
откуда и можно найти внутренние усилия.
Для части стержня слева от сечения:
Qx = - Rcx = å Ci; Mx = å Mx (Ri); ü
Qy = - Rcy = å Ui ; My = å My (Ri); ý (1.1)
Nz = Rcz = - å Zi; Mz = - å Mz (Ri). þ
Компоненты этих усилий называются так:
Qx, Qy - поперечные силы;
Nz - продольная или нормальная сила;
Mx, My - изгибающие моменты;
Mz - крутящий момент.
Внутренние усилия можно выразить не только через внешние силы и их проекции – по формуле (1.1), но и через компоненты вектора напряжения в поперечном сечении бруса с площадью F:
Qx =  t zxdF; Mx = - s z × ydF;
Qy = t zydF; My = - s z × xdF;
Nz = s z dF; Mz = (t zx y - t zy x) dF.
|
(1.2)
Отметим, что формулы (1.2) справедливы для любой части бруса – как слева, так и справа от сечения. В отличие от этих формул, в (1.1) при переходе к рассмотрению правой части стержня нужно сменить все знаки на противоположные.
В зависимости от значений внутренних усилий различают несколько видов напряженно-деформированных состояний (НДС), некоторые из которых мы рассмотрим.
1. Центральным растяжением и сжатием (ЦРС) называется НДС, при котором Nz ¹ 0, а все остальные внутренние усилия равны нулю. ЦРС возникает в брусе, растягиваемом (сжимаемом) силами, приложенными к его торцам (рис. 1.11а).
2. Чистый изгиб соответствует НДС, при котором обращаются в нуль все компоненты внутренних усилий за исключением Mx (или My). Появляется в брусе при его изгибе двумя моментами, приложенными по торцам (рис. 1.11б).
3. Поперечный изгиб – это НДС, при котором Qy ¹ 0, Mx ¹ 0, а остальные компоненты равны нулю. Возникает, например, в брусе, опертом по концам и загруженном посредине силой (рис. 1.11в).
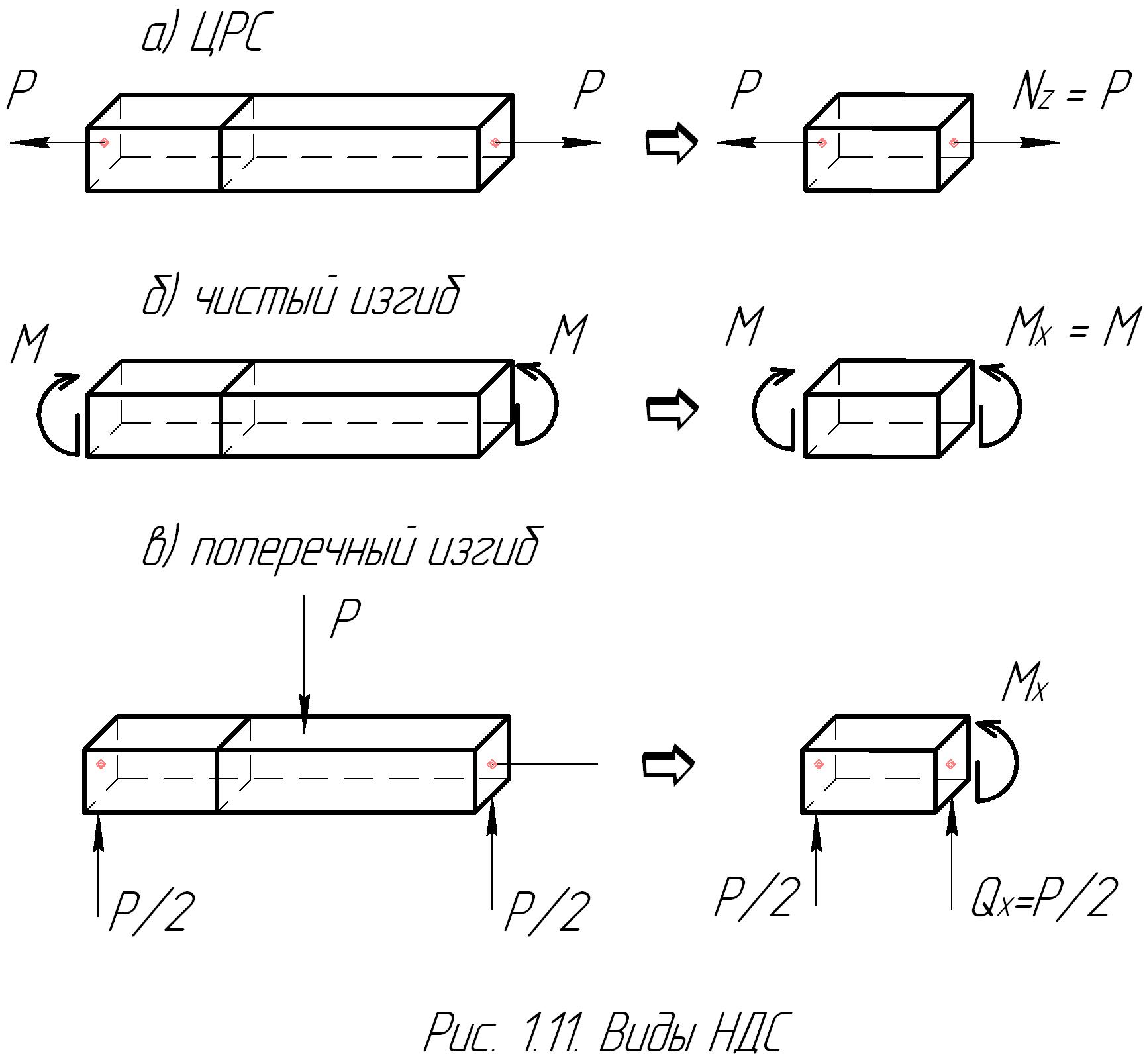
Решение основной задачи СМ для этих НДС бруса и составляет основное содержание данного раздела курса.
ПРИМЕЧАНИЯ:
1. В соответствии с принципом Сен-Венана картина распределения напряжений при ЦРС в поперечном сечении бруса на достаточном удалении от его концов не зависит от способа приложения нагрузки. Это справедливо и для других видов НДС.
2. Внутренние усилия, несмотря на название, не являются силами, противодействующими приложенной нагрузке, – по отношению к рассматриваемой части стержня продольная сила Nz является такой же внешней силой, как и сила Р (рис1.11а).
ГЛАВА 2. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ И СЖАТИЕ
2.1. Напряжения и деформации
Напряжения. Пусть стержень с площадью поперечного сечения F растягивается двумя равными по модулю силами Р.
Проведем сечение и рассмотрим часть стержня слева от сечения (рис. 1.11а). Действие отброшенной правой части заменим нормальными напряжениями s z, эквивалентными продольной силе Nz = Р.
Предполагая, что нормальные напряжения равномерно распределены по площади поперечного сечения F, получим:
Nz =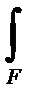 
s z dF = s z × F,
откуда искомое выражение для напряжений при ЦРС примет вид:
s z = Nz / F (2.1)
Правило знаков. При растяжении стержня: s z > 0, Nz > 0; при его сжатии –s z < 0, Nz < 0.
Деформации. Обозначим через l длину стержня до деформации, и пусть под действием приложенной нагрузки его длина стала равной l +D l, где D l - абсолютное удлинение стержня.
Относительным удлинением или продольной деформацией стержня при ЦРС называется величина
e = D l/l. (2.2)
Правило знаков. При растяжении: D l > 0, e > 0; при сжатии: D l < 0, e < 0.
В общем случае продольная сила Nz непостоянна по длине стержня. Например, – при его растяжении или сжатии под действием собственного веса. При этом будут неравномерны удлинения отдельных участков стержня и применение формулы (2.2) теряет смысл.
Для вывода формулы, являющейся обобщением (2.2) на случай переменной продольной силы и неравномерных деформаций, введем понятие перемещения точки деформируемого тела.
Пусть точка A (x, y, z) упругого тела в результате силовых или каких-либо иных воздействий перемещается и занимает в пространстве положение А'.
Вектор AA' (u, v, w)называется перемещением точки А деформируемого тела.
В общем случае каждая компонента вектора перемещения является функцией координат – x, y, z.
Рассмотрим брус длиной l в системе координат Oxyz, где начало отсчета выбрано на его левом, жестко защемленном конце, плоскость Oyz является плоскостью симметрии, а ось Оz проходит через центр тяжести сечений.
При этих предпосылках положение точки А, лежащей на оси бруса, однозначно определяется заданием только одной координаты – z (рис. 2.1а).
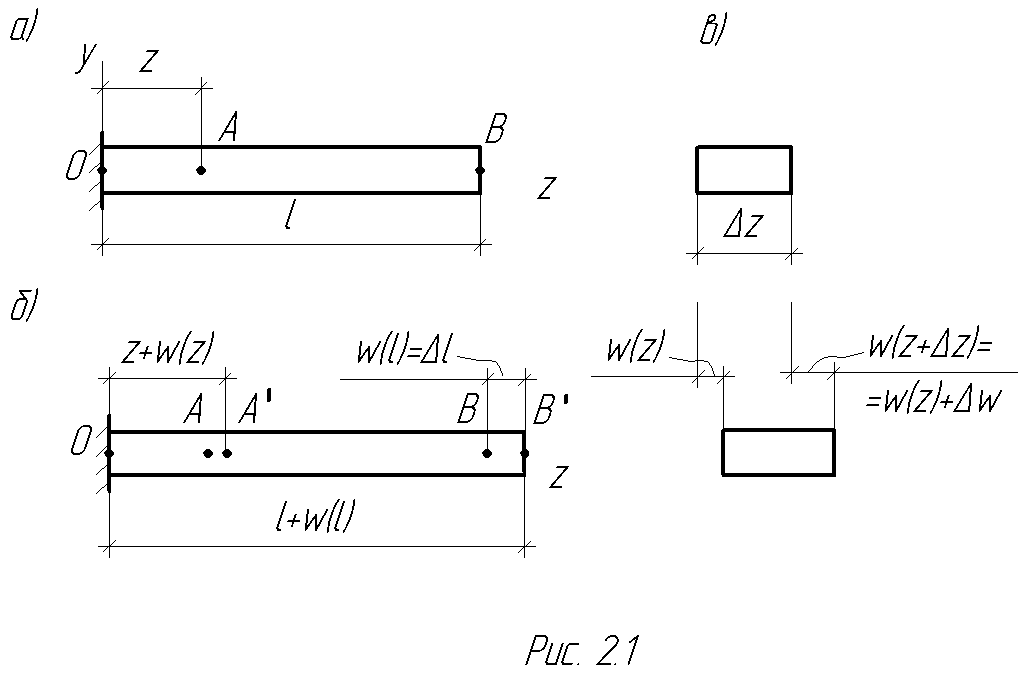
Под действием сил, приложенных вдоль оси Оz, и вызывающих центральное растяжение стержня, точка А получит перемещение AA'. Очевидно, что величина перемещения определяется удалением точки А от начала координат: w (0) = 0, w (z) = AA ¢, w (l) = D l (рис.2.1б).
Проведем два сечения на расстояниях z и z+ D z от левого конца и рассмотрим поведение заключенного между ними участка стержня в ходе его загружения. Если положить w (z +D z) = w (z) + D w, то станет очевидным, что перемещение этого отрезка стержня как твердого тела на величину w (z) сопровождается его удлинением на величину D w (рис. 2.1в). Предполагая, что продольная сила остается постоянной на участке D z, воспользуемся формулой (2.2) для определения его относительного удлинения. Подставляя в (2.2) D l = D w, а l = D z и переходя к пределу, получим выражение продольной деформации в сечении z:
e z =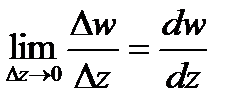 
. (2.3)
Таким образом, зная w (z) можно найти деформацию e z (z), и наоборот – по известной деформации e z из (2.3) можно найти перемещение w:
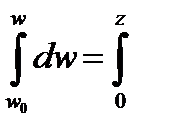e zdz,
или
w (z) = w 0 +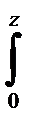 
e zdz. (2.4)
