Трапеция, описанная вокруг окружности

Примечание. Текст задачи взят с форума.

Задача.
Вокруг окружности описана равнобедренная трапеция, угол при основании которой равен 30 градусов. Высота трапеции равна 4 см. Найдите сумму длин оснований трапеции.

Решение.

Для решения данной задачи определим длину равных боковых сторон трапеции. По условию, угол KAB равен 30 градусам. Так как BK - высота равнобедренной трапеции, то треугольник ABK - прямоугольный. Откуда

BK / AB = sin 30

Значение sin 30 градусов найдем из таблицы тригонометрических функций.

BK / AB = 1/2
так как BK - высота трапеции, то
4 / AB = 1/2
AB = 8 см

Поскольку трапеция равнобокая (равнобедренная), то AB = CD = 8 см

Теперь обратимся к основному свойству четырехугольника, описанного вокруг окружности. Из него следует, что суммы длин противоположных сторон равны. То есть

AB + CD = BC + AD
откуда
BC + AD = 8 + 8 = 16 см

Что и требовалось определить.

Ответ: 16 см.

Параллелограмм

Параллелограмм - четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых.

Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Свойства параллелограмма

Противоположные стороны параллелограмма равны
Противоположные углы параллелограмма равны
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
Сумма углов, прилежащих к одной стороне, равна 180°.
Сумма всех углов равна 360°
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон

Признаки параллелограмма

Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий:

Противоположные стороны попарно равны
Противоположные углы попарно равны
Диагонали делятся в точке их пересечения пополам
Сумма соседних углов равна 180 градусов
Две стороны равны и параллельны

Площадь параллелограмма

Формулы нахождения площади параллелограмма приведены ниже:

То есть:

Площадь параллелограмма ABCD равна произведению длины одной из его сторон на высоту, опущенную на эту сторону
Площадь параллелограмма ABCD равна произведению двух его смежных сторон на синус угла между ними
Площадь параллелограмма ABCD равна половине произведения его диагоналей на синус угла между ними

Параллелограмм

Примечание. Это часть урока с задачами по геометрии (раздел параллелограмм). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение.

Задача.
Высоты параллелограмма равны 5см и 4см, а периметр равен 42см. Найдите площадь параллелограмма.

Решение.
Площадь параллелограмма равна произведению стороны на высоту, опущенную на эту сторону. Обозначим стороны параллелограмма как a и b.
Следовательно площадь и периметр будут равны:

S = 4a
S = 5b
P = 2a + 2b

Откуда 4a = 5b
a = 5/4b

Поскольку периметр параллелограмма равен 42 см, то
2(5/4b) + 2b = 42
b = 9 1/3

Откуда a = 11 2/3

Теперь находим площадь параллелограмма:
S = 4 * 11 2/3 = 5 * 9 1/3 = 46 2/3 см².

Ответ: 46 2/3 см².

Задача.
Периметр параллелограмма равен 16 см. Чему равны стороны параллелограмма, если известно, что одна его сторона в 3 раза больше другой

Решение.
У параллелограмма противоположные стороны равны, обозначим их как а и b, тогда периметр будет равен: Р = 2(а+b).
Пусть х - это сторона а, тогда

b=3х.
2(х+3х)=16
2*4х=16
х=2

значит сторона а=2, а сторона b=6.

Ответ: 2 и 6.

Параллелограмм (часть 2)

Задача

На диагонали МР прямоугольника МNРQ отложены равные отрезки МА и РВ. Докажите, что АNBQ параллелограмм.

Решение.

Четырехугольник является параллелограммом, если его противоположные стороны попарно равны. Докажем это.

Исходя из условия задачи треугольники MAN и PBQ равны. Так как PB = AM по условию задачи, PQ = NM как противоположные стороны прямоугольника, а углы BPQ и NMA равны, как внутренние накрест лежащие для параллельных прямых NP и MQ и секущей MP.

Аналогично доказывается равенство треугольников NBP и QAM.

Поскольку описанные треугольники равны, то NA = BQ, NB = BQ.

Таким образом, поскольку противолежащие стороны равны, то АNBQ параллелограмм.

Задача

В параллелограмме ABCD диагональ BD = 6 см и образует со сторонами AD и DC углы по 60 градусов. Определите углы и периметр параллелограмма ABCD.
Дополнительно: определите вид четырехугольника ABMD, где точка M - середина DC, определите углы четырехугольника ABMD.

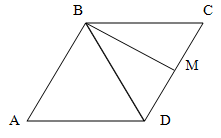
Решение.

Поскольку нам дана величина угла ADB (диагональ параллелограмма образует со сторонами AD и DC углы по 60 градусов), то величина угла DBC также равна 60 градусов, поскольку противоположные стороны параллелограмма параллельны, соответственно диагональ является секущей для двух параллельных прямых AD и BC, а для любой секущей внутренние накрест лежащие углы равны.

Таким образом, в треугольнике BCD нам известны два угла из трех, и они оба равны 60 градусов. Соответственно, поскольку сумма углов треугольника равна 180 градусов, то угол BCD также равен 60 градусам, из чего следует, что треугольник BCD - равносторонний.

Поскольку треугольник BCD - равносторонний, то BC = CD = BD = 6 см.

Таким образом, поскольку противолежащие стороны параллелограмма равны, периметр его равен 24 см. Параллелограмм является ромбом.

Дополнительно:

Поскольку точка М лежит на стороне CD, то AB и MD - параллельны, следовательно, ABMD - трапеция.

Угол DAB трапеции равен 60 градусов, исходя из решения, изложенного выше, как угол параллелограмма.

Угол ADM равен 120 градусов, так как по условию диагональ BD образует со сторонами AD и DC углы по 60 градусов, а ADM равен сумме данных углов.

Поскольку по условию точка M - середина DC, CM = MD. Значит BM - медиана треугольника DBC. Как указано выше, треугольник DBC - равносторонний, а в равностороннем треугольнике медиана является, одновременно, биссектрисой и высотой. Значит, угол DBM равен половине угла DBC и равен 60 / 2 = 30 градусов. Откуда угол ABM = 60 + 30 = 90 градусов. Поскольку BM - высота, то BMD равен также 90 градусов.

Исходя из сказанного, ABMD - прямоугольная трапеция.

Ответ: 24 см. 60º, 90º, 90º, 120º - прямоугольная трапеция.

Площадь параллелограмма

Примечание. Это часть урока с задачами по геометрии (раздел параллелограмм). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение.

См. также: Формулы, теоретический материал можно посмотреть по ссылке "Свойства и площадь параллелограмма".

Теоретический материал

Пояснения к формулам нахождения площади параллелограмма:

Площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную на эту сторону
Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними
Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними