Задача.
Докажите что биссектрисы острых углов прямоугольного треугольника при пересечении образуют угол 45.

Решение.
Поскольку сумма углов треугольника равна 180 градусам, угол С в данном случае прямой, то сумма двух оставшихся углов составляет 180 - 90 = 90 градусов.
Поскольку BM и AN - биссектрисы, а сумма их градусных мер составляет 90 градусов, то сумма половин этих углов (KAB и KBA) составляет 90 / 2 = 45 градусов. Таким образом, величина угла AKB в треугольнике AKB составляет 180 - 45 = 135 градусов.
Соответственно, величина угла MKA равна 180 -135 = 45 градусов. То есть биссектрисы прямоугольного треугольника образуют угол 45 градусов.
Таким образом, при пересечении биссектрисы прямоугольного треугольника образуют углы 45 и 135 градусов.
Применение теоремы Пифагора
Задача.
На вершинах двух елок сидят две вороны. Высота елок равна 4 м и 6 м. Расстояние между ними равно 10 м. На каком расстоянии BE нужно положить сыр для этих ворон, чтобы они находились в равных условиях, т.е. чтобы расстояния от них до сыра было одинаковым?
Решение.
Составим схему задачи.
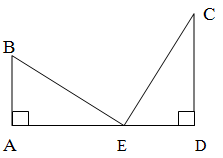
Поскольку ели растут вертикально, то AEB и DEC - прямоугольные треугольники.
Откуда
AB2 + AE2 = BE2
CD2 + DE2 = CE2
Поскольку птицы должны быть в равных условиях, то BE = CE, откуда
AB2 + AE2 = CD2 + DE2
Из условия задачи мы знаем, что AB = 4, а CD = 6 (или наоборот, что не имеет значения), тогда
AE2 + 42 = DE2 + 62
AE2 + 16 = DE2 + 36
Поскольку, по условию задачи AE + DE = 10, то
AE = 10 - DE
тогда
(10 - DE)2 + 16 = DE2 + 36
100 - 20DE + DE2 + 16 = DE2 + 36
80 = 20DE
DE = 4
Откуда AE = 10 - 4 = 6
Исходя из этого, поскольку
AB2 + AE2 = BE2
42 + 62 = BE2
BE2 = 52
BE = 2√13
Таким образом, расстояние между воронами 2√13 м
Ответ: BE = 2√13 м
Высота в прямоугольном треугольнике
Задача.
В треугольнике ABC угол С - прямой. Перпендикуляр CD равен 6 см. AD на 2 см. больше BD. Площадь треугольника ABC равна 180 см в кв. Найти чему равны AC и BС.
Решение.

Пусть BD = x, тогда AD = x + 2
Площадь треугольника ABC равна сумме площадей треугольников ADC и BDC. Поскольку CD - высота, то оба эти треугольника также прямоугольные. Так как площадь прямоугольного треугольника равна половине произведения катетов, то площадь треугольника ABC будет равна:
CD * AD / 2 + CD * BD / 2 = 180
Подставим известные значения и обозначения переменной х.
6 (x + 2) / 2 + 6x / 2 = 180
3 (x + 2) + 3x = 180
6x + 6 = 180
6x = 174
x = 29
Таким образом, BD = 29, AD = BD + 2 = 29 + 2 = 31
По теореме Пифагора вычислим длину AC и BC.
BC2 = CD2 + BD2
AC2 = CD2 + AD2
откуда
BC2 = 292 + 62
AC2 = 312 + 62
AB = √877
AC = √997
Ответ: √877 и √997
Высота в прямоугольном треугольнике (Часть 2)
Примечание. См. также формулы площади треугольника.
Задача
Площадь прямоугольного треугольника равна S, а один из острых углов равен α. Найти высоту, опущенную на гипотенузу.
Решение.

Площадь треугольника (S) будет равна:
S = 1/2 CD * AB
Пусть угол А равен α. Тогда
AC = AB cos α
(По определению косинуса cos α = AC /AB)
Рассмотрим треугольник ADC. Поскольку CD - высота, опущенная на гипотенузу, то угол CDA - прямой. Таким образом
CD = AC sin α
поскольку AC = AB cos α, то
CD = AB cos α sin α
откуда
AB = CD / (cos α sin α)
Вернемся к изначальной формуле площади прямоугольного треугольника и подставим в нее найденные значения.
S = 1/2 CD * AB
S = 1/2 CD * CD / (cos α sin α)
S = 1/2 CD2 / (cos α sin α)
Поскольку все значения, кроме высоты CD треугольника нам известны, выразим высоту из формулы площади прямоугольного треугольника.
CD2 = 2S cos α sin α
или
CD = √ (2S cos α sin α)






