Две прямых в пространстве могут занимать различное положение друг относительно друга: пересекаться, быть параллельны и скрещиваться.
1. Пересекающиеся прямые (рис. 3.11) имеют общую точку, проекции которой К 1 и К 2 расположены на одной линии связи.
2. Параллельные прямые пересекаются в несобственной точке. На эпюре одноименные проекции параллельных прямых параллельны, т.е. если a || b, то a 1 || b 1, a 2 || b 2, a 3 || b 3 (рис. 3.12).
Для прямых общего положения их параллельность определяется двумя проекциями. Особый случай представляют собой прямые параллельные одной из плоскостей проекций. Например, горизонтальные и фронтальные проекции профильных прямых всегда параллельны. Для оценки взаимного положения следует построить их проекции на p3. В данном примере прямые АВ и CD параллельны.

рис 3.11. Пересекающиеся прямые.

Рис. 3.12. Параллельные прямые.
Скрещивающиеся прямые не имеют общей точки, а точки пересечения их одноименных проекций не лежат на одной линии связи (рис. 3.13).
Исключение составляет случай, когда одна из скрещивающихся прямых профильная, и для оценки взаимного положения требуется построение проекции на плоскость p3. В данном примере BE и AC скрещиваются. Точки пересечения проекций скрещивающихся прямых лежащие на одной линии связи называются конкурирующими. По конкурирующим точкам определяется видимость элементов прямых на соответствующих плоскостях проекций.

Рис. 3.13. Скрещивающиеся прямые.
Видимость точек 1 и 2 на горизонтальной плоскости проекций определяется по фронтальной проекции, какая из точек по линии связи расположена выше (указано стрелкой). В данном случае точка 1, принадлежащая прямой а видима на p1.
Видимость точек 3 и 4 на фронтальной плоскости проекций определяется по горизонтальной проекции, какая из точек по линии связи расположена ближе к наблюдателю (указано стрелкой). В данном случае точка 3, принадлежащая прямой b видима.
Вопросы и задачи для самоконтроля
Когда след прямой будет находиться в бесконечно удаленной, несобственной точке?
Для какой прямой на эпюре следы:
a) лежат на оси проекций;
b) совпадают.
Построить следы прямой, определяемой точками А и В:
a) А (10, 20, 50); В (20, 50, 10).
b) А (60, 25, 60); В (20, 10, 25).
c) А (10, 15, 50); В (50, 15, 10).
ГЛАВА 4. ПЛОСКОСТЬ
Способы задания плоскости
Плоскость считается заданной; если из всех точек пространства можно выделить только те точки, которые принадлежат данной плоскости. Плоскость на чертеже может быть определена следующими способами (каждый из способов допускает переход к любому другому способу).
1. Тремя точками, не лежащими на одной прямой (рис. 4.1а).
2. Прямой и точкой вне прямой (рис. 4.1б).
3. Двумя пересекающимися прямыми (рис. 4.1в).
4. Двумя параллельными прямыми (рис. 4.1г).
5. Любой плоской фигурой-отсеком пространства (рис. 4.1д).

Рис. 4.1а. Три точки.

Рис. 4.1б. Прямая и точка.

Рис. 4.1в. Пересекающиеся прямые.
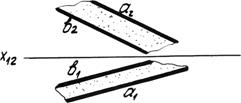
Рис. 4.1г. Параллельные прямые.

Рис. 4.1д. Фигура.
6. Следами плоскости (рис. 4.2).
Следы плоскости - это линии пересечения плоскости с плоскостями проекций.
Линия пересечения плоскости с плоскостью p1 называется горизонтальным следом плоскости Q 1, с плоскостью p2-фронтальным следом Q 2, с плоскостью p3-профильным следом Q 3. Точки пересечения следов на осях проекций называются точками схода следов Q x, Q y, Q z.
Отрезки OQ x, OQ y, OQ z, отсекаемые осями проекций, называют параметрами плоскости (рис. 4.2).

Рис. 4.2. Следы плоскости.






