В практике для изображения геометрических объектов, решения некоторых задач возникает необходимость использовать третью плоскость проекций p3, перпендикулярную p1 и p2. p3 – профильная плоскость проекций. А 3 – профильная проекция точки А.
Система трех плоскостей проекций делит пространство на 8 октантов, которые условно обозначают согласно рис. 2.3.

Рис. 2.3. Система 3х плоскостей проекций.
В первом октанте все координаты положительные.
Чтобы перейти к чертежу на плоскости, совместим все три плоскости в одну плоскость p2 по направлениям, указанным на чертеже. Плоскость p1 вращаем вокруг оси x 12 на 90°, плоскость p3 – вокруг оси z 23 на 90° против часовой стрелки. При этом ось y раздваивается.
Получается комплексный чертеж точки (рис. 2.4).

Рис. 2.4. Комплексный чертеж.
На комплексном чертеже все проекции точки А 1, А 2, А 3 находятся в проекционной связи. Каждая проекция точки определяется двумя координатами:
А 1 – x, y 1
А 2 – x, z
A 3 – y 3, z
В данном примере x = 30, y = 25, z = 35. Третья профильная проекция точки может быть определена по линиям связи от проекций А 1 и А 2. Проекции А 2 и А 3 расположены на одной горизонтальной линии связи, которая определяется координатой z (отрезок OA z), а от горизонтальной проекции А 1 проводим линию связи перпендикулярно оси y 1, отрезок OA y (координата y) переносим против часовой стрелки на горизонтальную ось y 3 и восставляем перпендикуляр (линию связи) до пересечения с горизонтальной линией связи от А 2. Координата у от А 1 переносится на горизонтальную ось у 3 всегда против часовой стрелки, т.к. плоскость p3 при совмещении с p2 разворачивается против часовой стрелки.
Профильную проекцию А 3 можно определить, откладывая координаты на соответствующих осях проекций с учетом знака.
Знаки координат зависят от того, в каком октанте расположена точка.
| Координаты | Октанты | |||||||
| I | II | III | IV | V | VI | VII | VIII | |
| x | + | + | + | + | - | - | - | - |
| y | + | - | - | + | + | - | - | + |
| z | + | + | - | - | + | + | - | - |
2.3 Точки разных углов пространства.
Точки частного положения
Если точка не принадлежит ни одной плоскости проекций, она занимает общее положение.
Если точка расположена в плоскости проекций или на оси проекций, она занимает частное положение.
Рассмотрим ряд точек общего положения (рис. 2.5, 2.6).
Точка В (x = 30, y = 25, z = -35) – IV октант. Проекция В 1 расположена ниже оси x на положительном направлении оси у. Траектория В 2 расположена тоже ниже оси х на отрицательном направлении оси z. В 3 определяется по линиям связи от В 1 и В 2 или по координатам y = 25, z = -35.
Точка С (x = -30, y = 40, z = 30) – V октант. Проекция С 1 расположена справа от оси z на отрицательном направлении оси x и ниже оси х на положительном направлении оси у. Проекция В 2 расположена выше оси х на положительном направлении оси

Рис. 2.5. Точки в 4 и 5 октанте.

Рис. 2.6. Комплексный чертеж точек в 4 и 5 октантах.
z. С 3 определяется по линиям связи от С 1 и С 2 или по координатам y = 40, z = 30.
Рассмотрим точки частного положения, расположенные на плоскостях и осях проекций.
Если координата х = 0, то точка принадлежит плоскости p3.
Если координата у = 0, то точка принадлежит плоскости p2.
Если координата z = 0, то точка принадлежит плоскости p1.
Рассмотрим ряд точек частного положения (рис. 2.7, 2.8).

Рис. 2.7. Точки частного положения.
Точка D (x = 0, y = 30, z = 20) принадлежит плоскости p3 и совпадает с профильной проекцией D 3, проекции D 1 и D 2 расположены соответственно на осях у и z.
Точка Е (x = 30, y = 0, z = 35) принадлежит плоскости p2 и совпадает с фронтальной проекцией Е 2, проекции Е 1 и Е 3 расположены соответственно на осях x и z.
Точка К (x = 40, y = 25, z = 0) принадлежит плоскости p1 и совпадает с горизонтальной проекцией К 1, проекции К 2 и К 3 расположены соответственно на осях x и у.
Точка L (x = 0, y = 5, z = 40) расположена на оси z.

Рис. 2.8. Комплексный чертеж точек частного положения.
Вопросы и задачи для самоконтроля
Сколько проекций точки вполне определяют ее положение в пространстве?
Какая координата точки определяет ее расстояние:
a) до горизонтальной плоскости проекций p1;
b) до фронтальной плоскости проекций p2;
c) до профильной плоскости проекций p3?
Выполнить комплексный чертеж точек и указать, в каком октанте они расположены:
a) A (x = 50, y = -10, z = -30);
b) B (x = -40, y = -20, z = 35);
c) C (x = -20, y = -30, z = -45);
d) D (x = -30, y = 0, z = -50);
e) E (x = 0, y = -40, z = 25).
ГЛАВА 3. ПРЯМЫЕ ЛИНИИ
Проекции прямой линии
Прямая линия в пространстве может быть задана двумя точками. Поэтому эпюр прямой определяется эпюром принадлежащих ей точек.
Рассмотрим проекции прямой, заданной отрезком AB (рис. 3.1, 3.2).
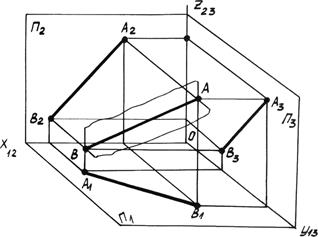
Рис. 3.1. Прямая общего положения.
А 1 В 1 – горизонтальная проекция прямой;.
А 2 В 2 – фронтальная проекция прямой;.
А 3 В 3 – профильная проекция прямой.
Две проекции прямой вполне определяют ее положение в пространстве. По рис. 3.1 каждая из проекций прямой определяет плоскость, перпендикулярную плоскости проекции (например, А 1 В 1 АВ, А 2 В 2 АВ), которые пересекаются по линии являющейся прямой АВ.

Рис. 3.2. Комплексный чертеж прямой общего положения.
Прямая, определяемая отрезком АВ, непараллельная ни одной из плоскостей проекций и является прямой общего положения. Проекции такой прямой расположены к осям проекций произвольно.




