Введение.
Начертательная геометрия является основой графической грамотности, необходимой для современного уровня технического творчества. Она развивает логическое мышление и пространственное воображение, способность по плоскому изображению мысленно представлять форму предмета. Начертательная геометрия изучает методы изображения пространственных фигур по чертежу и алгоритмы решения позиционных, метрических и конструкционных задач.
Аппаратом начертательной геометрии является чертежно-графическая модель существующих или задуманных предметов реального мира. Изучение начертательной геометрии способствует развитию пространственного воображения, логического мышления, совершенствует способность читать чертежи пространственных форм.
Современные инженеры, работающие в различных областях промышленности должны владеть теоретическими основами геометрического моделирования, уметь читать и анализировать чертежи. Знание, умение и навыки, приобретенные при изучение начертательной геометрии необходимы для изучения общеинженерных и специальных технических дисциплин, а также в последующей инженерной деятельности.
Данное учебное пособие содержит теоретический материал по начертательной геометрии, контрольные вопросы и задания для самостоятельного решения и демонстрирует возможности использования ПЭВМ для решения ряда задач начертательной геометрии и черчения.
Учебное пособие рекомендуется студентам технических вузов направления «Экономика и управление на предприятии» (060800), а также для студентов общетехнических факультетов.
Пособие разработано в соответствии с учебной программой по курсу «Основы геометрического моделирования» для специальности 060800 и «Инженерная и машинная графика» для специальностей 210100, 210200.
Обозначения и символы
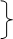A, B, C, D,…
- точки.
1, 2, 3, 4,…
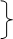A1, B1, C1,…
- проекции точек.
11, 21, 31,,…
a, b,c, … - прямые линии.
(AB) - прямая линия определяемая точками А и В.
a1, b1, … (A1B1) - проекции прямых линий.
x, y, z - оси координат.
p1, p2, p3 - плоскости проекций.
S(сигма), T(тау), G(гамма), D(дельта) -плоскости, поверхности.
(АВС) - плоскость определяемая точками А, В, С.
А1, А2, А3 - объект после последовательных преобразований.
a, b, j - углы.
Ç - пересечение.
|| - параллельность.
^ - перпендикулярность.
- скрещивание
Ì - взаимная принадлежность объектов (инцидентность)
º - совпадение, тождество.
® - логическое следствие.
ГЛАВА 1. СПОСОБЫ ПРОЕЦИРОВАНИЯ
Общие понятия метода проецирования
Операция проецирования является основой построения любого изображения.
Метод проекций заключается в проецировании каждой точки геометрического объекта на плоскость.
Рассмотрим точку А - геометрический объект. Зададим некоторую плоскость p - плоскость проекций и точку S, не принадлежащую p - центру проекций (рис. 1.1). Спроецируем точку А на плоскость p, проведем через точки S и А проецирующую прямую SA. Точка А pпересечения Рис. 1.1.
проецирующей прямой SA с плоскостью p есть проекция точки А. Плоскость p и центр S – аппарат проецирования. В зависимости от выбора аппарата проецирования различают центральное и параллельное проецирование.
Центральное проецирование
Аппаратом центрального проецирования является плоскость проекции p и центр проецирования точка S, причем S не принадлежит p. Сущность способа в том, что все проецирующие лучи исходят из центра S.
Рассмотрим ряд произвольных точек и определим их центральные проекции (рис. 1.2).
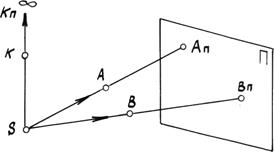
Рис. 1.2. Центральное проецирование.
Для этого из центра S через точки проведем проецирующие лучи до пересечения с плоскостью проекций. A p и B p– проекции точек А и В на плоскость проекций p.
Если для некоторой точки К проецирующий луч оказался параллелен плоскости проекций p, то проекция К p находится в несобственной точке, т.е. К p удалена в бесконечность.
