Прямая линия перпендикулярна плоскости, если она перпендикулярна любым двум пересекающимся прямым плоскости.
Однако распознать перпендикулярность прямой линии и плоскости в общем случае сложно, т.к. прямой угол проецируется на плоскость проекции в натуральную величину, когда одна из его сторон параллельна данной плоскости проекций. Следовательно, если на некоторой плоскости å (рис. 4.19) провести две пересекающиеся прямые, одна из которых горизонталь h || p, а другая - фронталь f || p2, то перпендикулярная к плоскости å прямая a проецируется на плоскость p1 перпендикулярно h 1, а плоскость p2 перпендикулярна f 2.
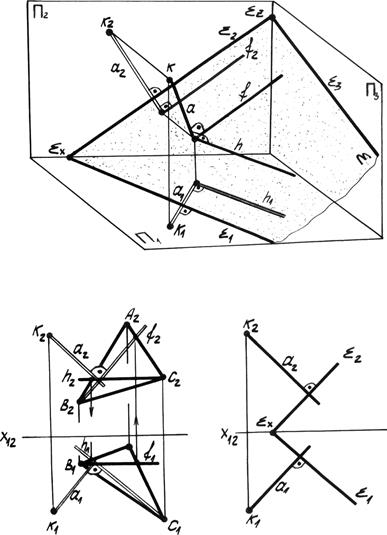
Рис. 4.19. Прямая линия, перпендикулярная плоскости.
Итак: если прямая линия перпендикулярна к плоскости, то её горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали, а её фронтальная проекция – перпендикулярна фронтальной проекции фронтали, а также к одноимённым следам.
На рис. 4.19 рассмотрены случаи построения перпендикуляра из точки K к треугольнику АВС и к плоскости å, заданной следами. Если плоскости заданы не следами, то первоначально всегда требуется определить горизонталь и фронталь в плоскости.
Взаимно перпендикулярные плоскости.
Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.
Для построения плоскости перпендикулярной к данной достаточно определить прямую линию ей перпендикулярную. Через перпендикуляр к плоскости можно провести множество плоскостей, перпендикулярных данной (рис. 4.20а).
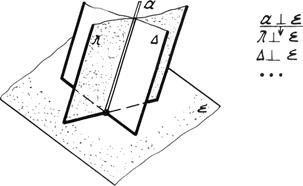
Рис. 4.20а. Взаимно перпендикулярные плоскости.
Рассмотрим построение одной из плоскостей, перпендикулярной данной плоскости (c Ç d) (рис. 4.20б).

рис. 4.20б. Взаимно перпендикулярные плоскости.
Определим горизонталь h и фронталь ¦ данной плоскости. Из произвольной точки K восставим перпендикуляр a на горизонтальной проекции a 1 ^ h 1, а на фронтальной проекции a 2 ^ ¦2. Дополним прямую a до плоскости пересекающейся с ней произвольной прямой b. Плоскость (a Ç b) перпендикулярна плоскости (c Ç d).
Вопросы и задачи для самоконтроля
1. Какими способами можно задать плоскость на чертеже?
2. Как можно перейти от любого способа задания плоскости к способу задания следами?
3. При каких условиях точка и прямая принадлежат плоскости?
4. Какие прямые линии в плоскости называются главными, и как они направлены?
5. Сформулируйте условия параллельности прямой линии плоскости и условия параллельности плоскостей.
6. Когда прямой угол между прямой линией и плоскостью проецируется в натуральную величину?
7. В каких случаях плоскости пересекаются по линиям частного положения:
a) прямыми уровня;
b) проецирующими прямыми.
8. Определите линию пересечения двух плоскостей, заданных параллельными прямыми (a || b) и пересекающимися прямыми (c || d) (задать самостоятельно).
9. Определите точку пересечения прямой (общего положения) с плоскостью S (общего положения.)






