Рассмотрим электрическую цепь, состоящую из источника питания, активного сопротивления и емкости, включенных последовательно. Эквивалентная схема такого двухполюсника приведена на рис. 15а.
Пусть по данной цепи проходит ток:
(1)
По второму закону Кирхгофа подводимое к этому двухполюснику напряжение равно сумме напряжений на отдельных участках цепи. В комплексной форме для действующих значений напряжений можно записать:
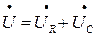(2)
Учитывая значения комплексных напряжени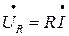й 
и 
, получим комплексное действующее значение напряжения на входе
(3)
Из уравнения (3) можно записать формулу закона Ома в комплексной форме:
(4)
Z – комплексное полное сопротивление:
(5)
где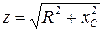 
- модуль полного сопротивления, 
(6)
- его аргумент.
Подставим в формулу (3) значение Z и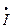 
, получим:
(7)
Из (7) определим модуль напряжения и его начальную фазу:
, 
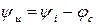(8)
Начальная фаза напряжения 
меньше начальной фазы тока 
на угол сдвига фаз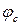 
. Следовательно, напряжение на входе емкостного двухполюсника отстает по фазе от тока на угол сдвига фаз .
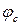На рис. 15б приведена векторная диаграмма емкостного двухполюсника. Для упрощения принято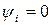 
, тогда вектор тока 
совпадет с осью +1. Активное падение напряжения 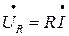совпадает по фазе с током, а вектор емкостного напряжения 
отстает от тока на 
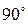. Вектор подводимого напряжения 
равен геометрической сумме векторов: 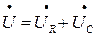. Он отстает от тока на угол сдвига фаз 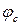. Если каждую из сторон треугольника напряжений разделить на ток , то получим треугольник сопротивлений (рис. 15в). Из него можно определить угол сдвига фаз по формуле:
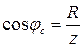(9)
Определим мгновенную мощность емкостного двухполюсника, полагая начальную фазу тока равной нулю:
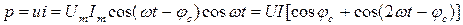(10)
Среднее значение мощности:
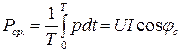(11)
Учитывая, что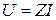 
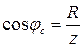, , то
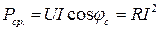(12)
Как и для индуктивного двухполюсника, среднее значение мощности емкостного двухполюсника равно его активной мощности.
Реактивная мощность характеризует амплитуду колебаний мощности обмена энергией между электрическим полем конденсатора и цепью:
(13)
Полная мощность
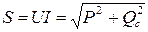(14)
Комплексная полная мощность
(15)
Из уравнения (15) следует, что реактивная емкостная мощность является отрицательной.
На рис. 16 построены графики мгновенных значений напряжения, тока (а) и мощности (б). Из графиков видно, что в промежутке времени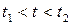 
, когда мощность положительна 
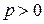, происходит одновременное преобразование энергии, поступающей от источника питания, в тепловую энергию и в энергию электрического поля 
.
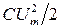В промежутки времени 
, когда мощность отрицательна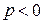 
, энергия частично возвращается обратно к источнику. В момент 
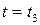к источнику возвращается энергия, равная заштрихованной площадке, ограниченной участком кривой и осью абсцисс.
