Гармонические колебания используются в радиовещании, в устройствах связи, в источниках питания, в модемах и т. д. Промышленное напряжение изменяется с частотой 50 Гц. Частоты порядка сотен и тысяч герц применяются в телефонных цепях, самые высокие частоты используются в радиоэлектронике: от 105 и 109 Гц.
Синусоида – единственная периодическая функция, имеющая подобную себе производную. Только при помощи синусоидальных токов можно сохранить неизменными формы кривых напряжений и токов во всех участках сложенной линейной электрической цепи. Это свойство синусоидальных токов позволит относительно просто производить расчет цепей переменного тока.
Гармонические колебание можно записать уравнениями с тригонометрическими функциями, изобразить графически или представить в виде векторов на декартовой или комплексной плоскости.
Пусть ток и напряжения изменяются по гармоническому закону:
 ,
, 
Значения аргументов синусоидальных функций  и
и  называются фазами синусоид. Значение фазы в начальный момент времени
называются фазами синусоид. Значение фазы в начальный момент времени  и
и  называют начальной фазой.
называют начальной фазой.
 Для расчёта электрических цепей аналитическое задание функции неудобно, так как алгебраические действия с тригонометрическими функциями громоздки.
Для расчёта электрических цепей аналитическое задание функции неудобно, так как алгебраические действия с тригонометрическими функциями громоздки.
Графическое представление синусоидальных величин (рис. 2) наглядно.
На графиках положительная начальная фаза  отчитывается влево от начала ординат, а отрицательная
отчитывается влево от начала ординат, а отрицательная  - вправо. Если у нескольких гармонических величин, изменяющихся с одинаковой частотой, начала синусоид не совпадают по времени, то они сдвинуты друг относительно друга по фазе. Разность углов
- вправо. Если у нескольких гармонических величин, изменяющихся с одинаковой частотой, начала синусоид не совпадают по времени, то они сдвинуты друг относительно друга по фазе. Разность углов  , равная разности начальных фаз, называется углом сдвига фаз. Угол сдвига фаз одноименных функций обозначают буквой
, равная разности начальных фаз, называется углом сдвига фаз. Угол сдвига фаз одноименных функций обозначают буквой  , а равноименных
, а равноименных  .
.
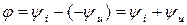 .
.
 Графическое представление синусоидальных величин из-за сложности построения синусоид применяют сравнительно редко. Изобразить гармонические величины можно векторами на декартовой плоскости (рис. 3). Совокупность векторов, изображающих синусоидальные э. д. с., напряжения и тока одной частоты, в соответствии со значениями их амплитуд и фазовых углов называют векторными диаграммами. Построение векторных диаграмм рационально начинать для начального момента времени t=0. В этом случае положение вектора определяется начальной фазой. На рис. 3 показаны векторные диаграммы напряжения и тока, изображенных синусоидами на рис. 2.
Графическое представление синусоидальных величин из-за сложности построения синусоид применяют сравнительно редко. Изобразить гармонические величины можно векторами на декартовой плоскости (рис. 3). Совокупность векторов, изображающих синусоидальные э. д. с., напряжения и тока одной частоты, в соответствии со значениями их амплитуд и фазовых углов называют векторными диаграммами. Построение векторных диаграмм рационально начинать для начального момента времени t=0. В этом случае положение вектора определяется начальной фазой. На рис. 3 показаны векторные диаграммы напряжения и тока, изображенных синусоидами на рис. 2.
 Применение векторных диаграмм делает анализ электрической цепи наглядным. В этом методе сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием их векторов.
Применение векторных диаграмм делает анализ электрической цепи наглядным. В этом методе сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием их векторов.
Расчёт цепей переменного тока облегчается, если изображать синусоидально изменяющиеся токи, напряжения, э. д. с. и т. д. комплексными числами. На комплексной плоскости ось абсцисс плоскости декартовых координат совмещают с осью вещественных или действительных значений (ось +1) комплексной плоскости. Ось ординат совмещают с осью мнимых чисел и величин (ось +  ). (В электронике мнимую единицу
). (В электронике мнимую единицу  обозначают
обозначают  ).
).
 Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в алгебраической, тригонометрической и показательной форме. Например, току
Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в алгебраической, тригонометрической и показательной форме. Например, току  , соответствует комплексное число записанные в алгебраической форме:
, соответствует комплексное число записанные в алгебраической форме:
 .
.
В тригонометрической форме:  .Используя подстановку Эйлера
.Используя подстановку Эйлера  , можно получить показательную форму записи
, можно получить показательную форму записи  .
.
Фазовый угол  определяется по проекциям вектора на оси координат +1 и +j:
определяется по проекциям вектора на оси координат +1 и +j:

Модуль комплексной амплитуды тока находится по формуле:

Мнимая составляющая комплексного числа вектора на комплексной плоскости определяет синусоидальное изменение сигнала и обозначается символом Im (Imagine – воображаемый), например,
 .
.
Действительная составляющая определяет косинусоидальное изменение сигнала и обозначается символом Re (Real – действительный)
 .
.
Комплексные величины  ,
,  называются комплексными амплитудами гармонического сигнала, которые содержат информацию об амплитуде и начальной фазе.
называются комплексными амплитудами гармонического сигнала, которые содержат информацию об амплитуде и начальной фазе.
Символический метод применяется для расчета. Он дает возможность выразить в алгебраической форме геометрические операции с векторами переменного тока, благодаря чему является возможным применять все методы расчета цепей постоянного тока для цепей переменного тока.






