Электрической схемой цепи называется рисунок, изображающий соединения реальных радиоэлементов. Электрические схемы используются при производстве радиоэлектронной аппаратуры. Для проведения расчетов используются эквивалентные схемы. Эквивалентная схема — это представление соединения и взаимосвязи реальных элементов с помощью идеальных элементов.
Структуру, конфигурацию цепи, порядок соединения элементов называют топологией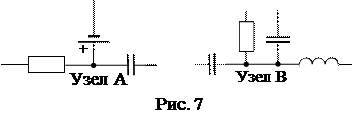 
электрической цепи. Анализируя схему цепи, можно выделить следующие топологические элементы.
Узел— это место (точка) соединения нескольких элементов цепи. Два узла, А и В, показаны на рис. 7. Узел, возникающий при соединении двух элементов, можно при расчетах объединить в один элемент.
Ветвь — это часть цепи, которая включена между узлами (рис. 8). Ветвь может состоять из одного элемента. Ветвь обозначают отрезком линии. Как правило, несколько ветвей при расчетах можно объединять в одну ветвь (рис. 8).
Представление цепи в виде совокупности ветвей и узлов называется графомцепи. Граф цепи отражает топологию или структуру цепи. Пример графа цепи, содержащего пять ветвей и четыре узла, показан на рис.9. Как правило, узел, к которому подключается максимальное число ветвей, считается нулевым узлом.
Контур цепи – это замкнутый путь из ветвей. Например, в цепи на рис.9 имеется три контура, образованных следующими наборами ветвей: (a,b,c), (c,d,e) и (a,b,d,e).
Для описания взаимосвязи токов и напряжений на разных ветвях используются уравнения соединений(законы Кирхгофа). Законы Кирхгофа установлены на основании многочисленных опытов и являются следствием закона сохранения энергии.
Первое уравнение соединений (первый закон Кирхгофа)устанавливает взаимосвязь токов в узле (рис. 10). 
В узле заряды не могут накапливаться или исчезать. Для узла выполняется закон сохранения заряда — сколько зарядов переносится к узлу втекающими токами, столько же зарядов выходит из узла. Согласно первому закону Кирхгофа (первое уравнение соединений):
алгебраическая сумма токов в узле равна нулю: 
,
где втекающие токи берутся со знаком плюс, а вытекающие — со знаком минус или наоборот. Например, для узла, изображенного на рис. 10, получим: 
.
Второе уравнение соединений (второй закон Кирхгофа)устанавливает взаимосвязь напряжений и ЭДС в контурах цепи.
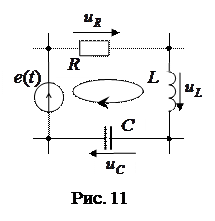По второму закону Кирхгофа в замкнутом контуре (рис.11) алгебраическая сумма ЭДС равна сумме напряжений на отдельных участках цепи: 
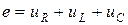. Если стрелка напряжения или ЭДС противоположна направлению обхода, то эти ЭДС или напряжение должны записываться в формулу со знаком минус.
Для контура, включающего 
ЭДС и 
ветвей, используется следующая математическая запись второго закона Кирхгофа
,
где при согласованных стрелках направления обхода и напряжения на ветви или ЭДС ставится плюс, а при несогласованных – минус.
Рассмотрим использование этих уравнений для описания процессов в цепи, схема которой изображена на рис. 12. Записывая для контура этой цепи второй закон Кирхгофа: 
, и учитывая уравнения элементов, получим интегро-дифференциальное уравнение цепи:
.
Дифференцируя это выражение, получим дифференциальное уравнение электрической цепи для одной из неизвестных величин – тока цепи:
.
Коэффициенты этого уравнения являются константами и определяются параметрами элементов схемы. В правой части таких уравнений записываются члены, содержащие заданные токи или напряжения. Полученное выражение называется неоднородным линейным дифференциальным уравнением цепи.
Для линейной электрической цепи справедлив принцип суперпозиции (наложения). В цепи, включающей последовательно соединенные резистор, катушку и конденсатор, действуют два сигнала: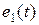 
и 
. В контуре цепи как реакция на эти два сигнала возникает результирующий ток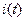 
.
Пусть на цепь воздействует только один сигнал 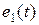(сигнал равен нулю). Дифференциальное уравнение для тока 
, возникающего под действием ЭДС 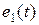, имеет вид
.
Пусть теперь напряжение 
равно нулю и на цепь воздействует сигнал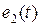 
. Дифференциальное уравнение для тока 
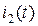, возникающего под действием ЭДС 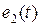, имеет аналогичный вид
.
Суммируя левые и правые части этих уравнений окончательно получим.
.
Из анализа формулы следует, что сумма сигналов 
вызывает появление реакции — результирующего тока 
, равного сумме токов 
, возникающих от каждого из сигналов в отдельности. Обобщая полученные результаты на сложные линейные цепи при воздействии нескольких источников, получим принцип суперпозиции: реакция на сумму воздействий в линейной цепи равна алгебраической сумме реакций на каждое из воздействий в отдельности. Для нелинейных цепей принцип суперпозиции несправедлив.
Глава 2.
