
Простой и широко используемой в радиоэлектронике линейной системой с постоянными параметрами является колебательный контур, содержащий емкость C, индуктивность L и сопротивление R (рис. 1). Сопротивление R учитывает сопротивление потерь конденсатора и индуктивности.
Пусть в момент времени t=0 конденсатор имеет заряд 
 . Найдем закон изменения во времени заряда на конденсаторе.
. Найдем закон изменения во времени заряда на конденсаторе.
По закону Кирхгофа:
 (1)
(1)
В контуре действует только ЭДС самоиндукции  , поэтому:
, поэтому:
 (2)
(2)
Напряжение равно сумме напряжений на активном резисторе и емкости:
 (3)
(3)
Подставим в уравнение (1) уравнения (2) и (3), получим:

 (4)
(4)
Разделим (4) на L ( ) и, обозначив через
) и, обозначив через  ,
, 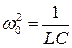 , (
, ( - коэффициент затухания,
- коэффициент затухания,  -собственная частота) получим:
-собственная частота) получим:
 (5)
(5)
Уравнение (5) линейное, однородное, дифференциальное уравнение описывает свободные колебания в контуре с учетом потерь энергии в отсутствие внешних воздействий. Общее решение уравнение (5) будем искать в виде:
 (6)
(6)
где  -корни характеристического уравнения
-корни характеристического уравнения  , т.е.
, т.е.
 (7)
(7)
При этом различают три случая:
а)  - случай малого сопротивления,
- случай малого сопротивления,
б)  - случай большого сопротивления,
- случай большого сопротивления,
в)  - предельный случай.
- предельный случай.
а)  или
или 
Учитывая, что волновое сопротивление  , последнее неравенство может быть записано так
, последнее неравенство может быть записано так 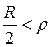 .
.
Для этого случая решение уравнения (5) имеет вид:
 (8)
(8)
Колебания, описываемые формулой (8) представляют собой свободные затухающие колебания. Эти колебания не являются периодическими, т.к. выражение  переменно и убывает по экспоненциальному закону (рис. 2.а).
переменно и убывает по экспоненциальному закону (рис. 2.а).
Однако, по аналогии со свободными колебаниями и здесь вводят частоту и период колебаний.
Частота колебаний тока в контуре при наличии сопротивления равна:

 (9)
(9)
т.е.  .
.
Период колебаний T при наличии сопротивления цепи равен:


Для идеального контура 
 , тогда
, тогда
 (10)
(10)
Период затухания колебаний больше периода собственных колебаний. Если  , тогда
, тогда  .
.
Решение (8) можно представить графически (рис. 2а).
б)  . В этом случае
. В этом случае  . В контуре совершается затухающее апериодическое колебание согласно уравнению:
. В контуре совершается затухающее апериодическое колебание согласно уравнению:
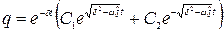 (11)
(11)
Вследствие изменения по показательному закону, колебание быстро затухает. Характер колебаний зависит от начальных условий. Если 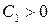 , а
, а  , то графическое решение уравнения (11) имеет вид, представленный на (рис. 2б). Конденсатор С цепи успевает один перезарядиться.
, то графическое решение уравнения (11) имеет вид, представленный на (рис. 2б). Конденсатор С цепи успевает один перезарядиться.
в)  , тогда
, тогда  .
.
Решение дифференциального уравнения (5) находят в виде:
 (12)
(12)
На рис. 2в представлено графическое изображение уравнения (12).
Обычно в колебательном контуре потери энергии таковы, что выполняется условие а). Для реализации условий б) и в) вводят в контур добавочное сопротивление.
К величинам, характеризующим быстроту затуханий колебаний в колебательном контуре, относятся коэффициент затухания  , логарифмический декремент затухания d, добротность Q.
, логарифмический декремент затухания d, добротность Q.
1. Коэффициент затухания  характеризует быстроту затухания колебаний в контуре. Для выяснения физического смысла
характеризует быстроту затухания колебаний в контуре. Для выяснения физического смысла  , возьмем интервал времени
, возьмем интервал времени 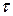 , такой, чтобы по его истечению амплитуда колебаний уменьшалась в e раз:
, такой, чтобы по его истечению амплитуда колебаний уменьшалась в e раз:
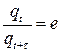 , (13)
, (13)
при этом совершается N целых колебаний:
 (14)
(14)
В момент времени t заряд изменяется по закону:
 (15)
(15)
В момент времени  измерение заряда равно:
измерение заряда равно:
 (16)
(16)
Подставив (14) и (15) в (13), получим:
 .
.
Сравнивая показатели степени, имеем:

 (17)
(17)
Таким образом, коэффициент затухания  есть временная характеристика, величина, обратная тому промежутку времени
есть временная характеристика, величина, обратная тому промежутку времени 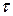 , по истечении которого амплитуда колебаний в контуре уменьшается в e раз.
, по истечении которого амплитуда колебаний в контуре уменьшается в e раз.
2. Логарифмический декремент затухания d.
Декремент затухания характеризует уменьшение амплитуды колебаний за период  . Логарифмический декремент затухания d равен натуральному логарифму этого отношения:
. Логарифмический декремент затухания d равен натуральному логарифму этого отношения:
 (18)
(18)
 (19)
(19)
Учитывая формулу (19), получим:
 (20)
(20)
Формула (20) выражает связь d с параметрами контура.
Если  , то
, то
 (21)
(21)
Выясним физический смысл логарифмического декремента затухания d. Для этого из формулы (14) найдем период, подставим его значение в формулу (19) и учитывая (17), получим:
 (22)
(22)
Логарифмический декремент затухания числовая характеристика, величина, обратная тому числу полных колебаний, по истечении которых амплитуда колебаний уменьшается в e раз.
Чем меньше d, тем большее число колебаний совершится до их полного затухания. Запасенная энергия в контуре определяется выражением:
 (23)
(23)
Энергия, израсходованная контуром за половину периода:
 (24)
(24)
В течение периода можно считать, что ток изменяется по гармони-ческому закону, тогда:
 (25)
(25)
Найдем отношение:
 (26)
(26)
 (26а)
(26а)
Логарифмический декремент затухания  является обратной энергетической характеристикой: чем больше расход энергии при колебаниях и чем меньше запас энергии в контуре, тем больше
является обратной энергетической характеристикой: чем больше расход энергии при колебаниях и чем меньше запас энергии в контуре, тем больше  .
.
3. Добротность колебательного контура
 (27)
(27)
В (27) подставим формулу (20)
 , (28)
, (28)
если  , то
, то  .
.
Добротность контура равна отношению волнового сопротивления к активному; это безразмерная величина.
Добротность - это энергетическая характеристика контура. Подставим (25а) в (26), получим:
 (30)
(30)






