Построим график арксинуса 

Построим график арккосинуса 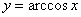

Построим график арктангенса 

Всего лишь перевернутая ветка тангенса.
Перечислим основные свойства функции  :
:

Свойства арккотангенса вы вполне сможете сформулировать самостоятельно. Отметим, что арккотангенс, как и арккосинус, не является четной или нечетной функцией.
При исследовании функции и изучении её свойств с целью построения графика находят: область определения функции D(f и, если возможно, область изменения E(f);
1) точки разрыва функции и промежутки непрерывности;
2) точки пересечения графика с осями координат;
3) промежутки знакопостоянства функции;
4) чётность, нечётность, периодичность;
5) критические точки функции, точки экстремума, экстремумы, промежутки монотонности;
6) промежутки выпуклости, вогнутости графика функции, точки перегиба;
7) асимптоты графика функции;
8) дополнительные точки (если это необходимо).
Строится график функции. Примеры.
| Способ построения графиков функций по точкам: | |

| Вытекает из определения графика функции. Он является длинным и недостаточно надежным. Применяется в школьном курсе математики при первоначальном знакомстве с простейшими функциями. (На графике функция  ). ).
|
| Построение графиков функций на основании результатов исследования функции (без использования понятия производной) | ||||
Дана функция 
| преобразуем 
| |||
| 1. Область определения | 
| |||
| 2. Область значений | 
| |||
| 3. Четность, нечетность | 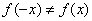 и и  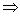 Ни четная, ни нечетная Ни четная, ни нечетная
| |||
| 4. Монотонность | Убывает во всей области определения 
| |||
5. Пересечение с осями  и и 
| 
| 
| ||
| 6. Промежутки знакопостоянства | 
| 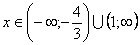
| ||

| 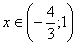
| |||
| 7. Берем дополнительные точки |

| |||
| По результатам исследований строим график | ||||
Да, конечно, данную кривую легко построить и поточечно, но такие параболы очень часто встречаются в практических заданиях, поэтому весьма полезно сразу представлять, как они расположены.
График функции y=Af(ax+b) может быть получен из графика функции y=f(x) с помощьюпростых геометрических преобразований. Приведем их в таблице:
| y=f(x)+A | Параллельный перенос его вдоль оси OY на А единиц вверх, если А>0 и на |A| единиц вниз, если A<0/ |
| y= f(x-a) | Параллельный перенос его вдоль оси ОY на a единиц вправо, если а>0, и на -а единиц влево, если a<0. |
| y=kf(x), k>0 | Растяжение вдоль оси ОХ в k раз, если k>1, и сжатие в 1/k раз, если 0<k<1. |
| y=f(kx), k>0 | Сжатие вдоль оси ОХ относительно оси OY в k раз, если k>1 и растяжение в 1/k раз, если 0<k<1. |
| y=-f(x) | Симметричное отображение графика относительно оси ОХ. |
| y=|f(x)| | Часть графика функции y=f(x), расположенная ниже оси ОХ, симметрично отражается относительно этой оси, остальная часть графика остается без изменения. |
| y=f(-x) | Симметричное отображение графика относительно оси ОY. |
| Y=f(|x|) | Часть графика функции y=f(x), расположенная в области x> 0, остается без изменения, а его часть для области x < 0 заменяется симметричным отображением относительно оси OY. |
Пример1. Чтобы построить график функции 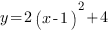 , нужно
, нужно
§ сначала построить график функции  ,
,
§ затем одинаты всех точек графика умножить на 2,
§ затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
§ а затем вдоль оси OY на 4 единицы вверх:

Пример 2.
Построить график функции 
И снова вечная картина:

Согласно правилу, при  график сохраняется:
график сохраняется:

И сохранившаяся часть отображается симметрично относительно оси  в левую полуплоскость:
в левую полуплоскость:
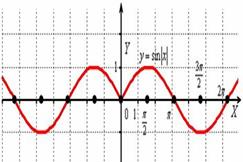
Действительно, функция  – чётная, и её график симметричен относительно оси ординат.
– чётная, и её график симметричен относительно оси ординат.






