| 1.Вариант (Вычислите интегралы)
| 2.Вариант (Вычислите интегралы)
| |||
| 
| 
| |||
| 
| 
|
Список литературы
1.http://www.allmathcad.com/ru/integral.html
ПРАКТИЧЕСКАЯ РАБОТА № 13
Прямые и плоскости в пространстве».
Цели урока:
1) Обобщить теоретические знания по теме: «Прямые и плоскости в пространстве».
2) Рассмотреть алгоритмы решений заданий теме «Прямые и плоскости в пространстве», решить задачи.
3) Формировать потребность к самопознанию; умение ставить цели и реализовывать их.
Теоретический материал
Основными геометрическими фигурами в пространстве являются точка, прямая и плоскость.
Через всякие три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.
Через любую прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.
Плоскость делит (разбивает) пространство на два полупространства.
Две плоскости в пространстве либо параллельны (т. е. не имеют общих точек), либо пересекаются по прямой.
Прямая либо параллельна плоскости (т. е. не имеет с ней рбщих точек), либо пересекает ее в одной точке, либо целиком лежит в плоскости.
Признак параллельности прямой и плоскости.
Если прямая параллельна какой-нибудь прямой, лежащей в плоскости, то она параллельна этой плоскости.
Две прямые в пространстве либо пересекаются (имеют одну общую точку), либо скрещиваются, либо параллельны
(на рис. прямые а и b пересекаются, прямые а, с и d параллельны, прямые b и d скрещиваются).
Через две пересекающиеся прямые можно провести плоскость, и притом только одну; то же справедливо и для параллельных прямых.
Через две скрещивающиеся прямые невозможно провести плоскость.
Признак параллельности прямых.
Две прямые, каждая из которых параллельна третьей прямой, параллельны между собой.
Прямая, пересекающая плоскость, называется перпендикулярной (ортогональной, или нормальной) этой плоскости, если она перпендикулярна всем прямым, лежащим в этой плоскости (рис.).
Если прямая перпендикулярна двум непараллельным прямым, лежащим в плоскости, то эта прямая перпендикулярна плоскости.
Пусть прямая пересекает плоскость в точке А и перпендикулярна плоскости; отрезок АВ этой прямой (рис.) называется перпендикуляром, проведенным (или опущенным) к этой плоскости из точки В.
Длина перпендикуляра АВ называется расстоянием от точки В до плоскости.
Из произвольной точки вне плоскости можно опустить на плоскость один перпендикуляр и множество наклонных (рис.).
Если АВ — перпендикуляр, ВС — наклонная, то АС — проекция наклонной на плоскость, точка С — основание наклонной, точка А — основание перпендикуляра.
Угол между прямой и плоскостью определяется как угол между этой прямой и ее проекцией на плоскость.
Теорема о трех перпендикулярах.
Прямая на плоскости перпендикулярна наклонной, если она перпендикулярна проекции этой наклонной (рис.). Верно и обратное утверждение.
Рассмотрим подробное решение нескольких стереометрических задач.
Задача 1.
Параллельные плоскости α и β пересекают стороны угла АВС в точках А1, С1, А2, С2 соответственно.
Найти ВС1, если А1В: А1А1 = 1: 3, ВС2 = 12.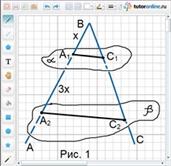 
Решение.
Рассмотрим рис. 1.
1) Так как А1В: А1А2 = 1: 3, то А1В = х, А1А2 = 3х.
2) Плоскость (АВС) пересекает плоскость α по прямой А1С1, а плоскость β – по прямой А2С2. Так как плоскости α и β параллельны, то параллельны и прямые А1С1 и А2С2.
3) Рассмотрим угол АВС. По теореме Фалеса выполняется:
ВА1/ВА2 = ВС1/ВС2.
Кроме того, ВА2 = ВА1 + А1А2, а значит, учитывая пункт 1
ВА2 = ВА1 + А1А2 = х + 3х = 4х.
Тогда х/(4х) = ВС₁/12, то есть ВС1 = 3.
Ответ: 3.
Задача 2.
В ромбе АВСD угол А равен 60°, сторона ромба равна 4. Прямая АЕ перпендикулярна плоскости ромба. Расстояние от точки Е до прямой DC равно 4. Найти квадрат расстояния от точки А до плоскости ЕDC.
Решение.
1) Проведем АН перпендикулярно DC (рис. 2), тогда ЕН перпендикулярно DC по теореме о трех перпендикулярах. Значит ЕН – расстояние от точки Е до прямой DC, то есть ЕН = 4.
2) Проведем АК – высоту треугольника АЕН – и докажем, что АК – расстояние от точки А до плоскости (ЕDC):
DC перпендикулярно АН и DC перпендикулярно ЕН, значит, DC перпендикулярно плоскости (АЕН) по признаку перпендикулярности прямой и плоскости. АК содержится в плоскости (АЕН), значит АК перпендикулярно DC. Кроме того, АК перпендикулярна ЕН по построению. Так как прямая АК перпендикулярна двум пересекающимся прямым, лежащим в плоскости ЕDC (ЕН и DC), то АК перпендикулярно плоскости (ЕDC), значит, АК – расстояние от точки А до плоскости (EDC).
3) Рассмотрим треугольник ADH: АD = 4, угол ADH = 60° (накрест лежащий с углом ВАD),
тогда АН = АD · sin ADH. Имеем, что АН = 4 · √3/2 = 2√3.
4) Рассмотрим треугольник ЕАН – прямоугольный (угол ЕАН = 90°). По теореме Пифагора
ЕН2 = ЕА2 + АН2;
ЕА2 = 16 – 12 = 4;
ЕА = 2.
Для площади треугольника ЕАН можно использовать формулы
SEAH = (EA · AH)/2 или SEAH = (AК · ЕH)/2, тогда
EA · AH = AК · ЕH или АК = (EA · AH)/ЕН.
Имеем: АК = (2 · 2√3)/4 = √3, поэтому АК2 = 3.
Ответ: 3. 
Задача 3.
В треугольнике АВС угол В – прямой, ВС = 2. Проекцией этого треугольника на некоторую плоскость является треугольник ВDC, АD = √2, угол между плоскостями АВC и ВСD равен 45°. Найти угол (в градусах) между прямой АС и плоскостью (ВDC).
Решение.
1) По теореме о трех перпендикулярах ВD перпендикулярно ВС, тогда угол между плоскостями (АВС) и (ВDC) – есть угол АВD равный 45° (рис. 3).
2) АС – наклонная, АD – перпендикуляр к плоскости (BCD), CD – проекция АС на плоскость (ВСD), значит угол АСD равен углу между прямой АС и плоскостью (ВDC), то есть угол АСD – искомый.
3) Рассмотрим треугольник АВD – прямоугольный (угол АВD = 90°):
АВ = АD/sin ABD;
AB = √2/(√2/2) = 2.
4) Рассмотрим треугольник АВС – прямоугольный (угол АВС = 90°). По теореме Пифагора
АС2 = АВ2 + ВС2;
АС2 = 4 + 4 = 8;
АС = 2√2.
5) Рассмотрим треугольник АСD – прямоугольный (угол ADC = 90°):
так как АD = 1/2 АС, то угол АСD = 30°.
Ответ: 30°.
