Найдите производные следующих функций:
1)  2)
2) 
3)  4)
4) 
5)  6)
6) 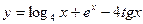
7)  8)
8) 
9)  10)
10) 
11)  12)
12) 
13)  14)
14) 
Найдите вторую производную:
1) 
2) 
3) 
4) 
Список литературы
1.http://www.exponenta.ru/soft/Maple/Maple.asp
ПРАКТИЧЕСКАЯ РАБОТА № 9
«Интеграл»
Цели урока:
1) Обобщить теоретические знания по теме: «Интеграл».
2) Рассмотреть алгоритмы решений заданий теме «Интеграл», решить задачи.
3) Формировать умение ставить цели и реализовывать их.
Теоретический материал
1.Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная

Неопределенный интеграл алгебраической суммы функций равен алгебраической сумме неопределенных интегралов этих функций

Постоянный множитель подынтегрального выражения можно выносить за знак неопределенного интеграла

3. Таблицы основных интегралов
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11. 
4. Рассмотрим примеры на применение формул:
1. 
Решение:
Введем новую переменную и сделаем подстановку
cosx= t
dcosx =dt
-sinx dx=dt откуда dx= 
После подстановки получим:

Вернемся к старой переменной:

2. 
Решение:
Введем новую переменную и сделаем подстановку
5-2х3= t
d(5-2х3)=dt
-6x2 dx=dt откуда dx= 
После подстановки получим:

Вернемся к старой переменной:

Задачи для самостоятельного решения
1. 
2. 
3. 
1. Приращение F(b) – F(a) любой первообразной для функции f(x) при изменении аргумента от x=a до x=b называется определенным интегралом от функции f(x) и обозначается:


2. А) Определенный интеграл алгебраической суммы функций равен алгебраической сумме определенных интегралов этих функций

Б) Постоянный множитель подынтегрального выражения можно выносить за знак определенного интеграла

В) При перестановке пределов интеграла знак интеграла меняется на противоположный,

3. Рассмотрим примеры на применение формул:
А) Метод непосредственного интегрирования
1. Вычислить

Решение:
Б) Метод подстановки
2. 
Решение:
Введем новую переменную и сделаем подстановку
5+2х3= t
d(5+2х3)=dt
6x2 dx=dt откуда dx= 
После подстановки получим:

Вернемся к старой переменной:
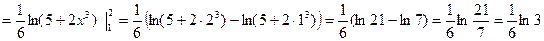
Задачи для самостоятельного решения

 1.
1.  1.
1. 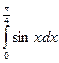

 2.
2.  2.
2. 

 3.
3. 

Список литературы
1. «Алгебра и начало анализа» под ред. ЯковлеваГ.Н. М., 2003г.
2. Башмаков М.М.. «Математика» М., 2004г.
3. Валуцэ И.И., Дилигул Г.Д. «Математика для техникумов» М., 1999г.
4. Ананасов П.Т., Орлов М.И. «Сборник задач по математике» М., 1987г.
ПРАКТИЧЕСКАЯ РАБОТА № 10
«Нахождение интегралов в среде Mathcad»
Цели урока:
1) Обобщить теоретические знания по теме: «Нахождение интегралов в среде Mathcad».
2) Рассмотреть алгоритмы решений заданий по данной теме, используя формулы вероятности событий, решить задачи.
3) Формировать умение планировать свою деятельность, умение ставить цели и реализовывать их.
Теоретический материал
Интеграл в Mathсad можно вычислить с помощью оператора интегрирования на панели  инструментов “ Исчисление ”. В результате активизируется шаблон определенного интеграла, который имеет четыре поля для ввода пределов интегрирования, переменной интегрирования и функции интегрирования. Результат вычисления определенного интеграла отображается после ввода знака равно “ = ”. При вычислении определенного интеграла для получения более точного и достоверного результата можно выбрать метод расчета путем вызова контекстного меню щелчком правой кнопки мыши по полю шаблона. По умолчанию активизирован режим “ автовыбор ”, при котором Mathcad автоматически выбирает один из методов.
инструментов “ Исчисление ”. В результате активизируется шаблон определенного интеграла, который имеет четыре поля для ввода пределов интегрирования, переменной интегрирования и функции интегрирования. Результат вычисления определенного интеграла отображается после ввода знака равно “ = ”. При вычислении определенного интеграла для получения более точного и достоверного результата можно выбрать метод расчета путем вызова контекстного меню щелчком правой кнопки мыши по полю шаблона. По умолчанию активизирован режим “ автовыбор ”, при котором Mathcad автоматически выбирает один из методов.
Метод Romberg (Ромберг) используется в Mathcad как общий метод для гладких функций; Adaptive (адаптивный) – для функций быстроизменяющихся на участке интегрирования; Infinie Limit (неограниченный лимит) – бесконечный предел – для расчета интегралов с бесконечными пределами интегрирования. Метод Singular Endpoint (сингулярный конец) применяется для расчета интегралов от функций, не существующих в одной или обеих точках пределов интегрирования (так называемые несобственные интегралы второго рода).
При необходимости пользователь может отказаться от режима “ автовыбор ” и принудительно указать в Mathcad нужный метод расчета. На листинге приведены примеры вычисления определенного интеграла. Как показывает анализ результатов расчета, режим автовыбор является наиболее универсальным при расчете определенного интеграла.







