Определение. Произведением двух комплексных чисел называется такое комплексное число, модуль которого равен произведению модулей сомножителей, а аргумент – сумме аргументов сомножителей.
Это определение совершенно очевидно, если использовать показательную форму комплексного числа:

Пусть комплексные числа даны в алгебраической форме. Найдём их произведение: (a 1 + b 1 i) (a 2 + b 2 i) = x + iy.
Имеем  .
.
Согласно определению умножения можем записать:
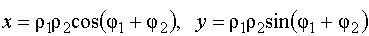 .
.
Распишем: 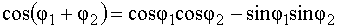 ,
,
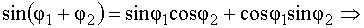

 ,
,

 .
.
Окончательно получим:
 .
.
Отсюда следует правило умножения комплексных чисел в алгебраической форме: комплексные числа можно перемножать как многочлены.
Если z = а + b i – комплексное число, то число 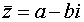 называется сопряжённым с числом z. Его обозначают при помощи черты над числом.
называется сопряжённым с числом z. Его обозначают при помощи черты над числом.
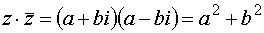 , но
, но  , следовательно,
, следовательно,  .
.
Деление комплексных чисел
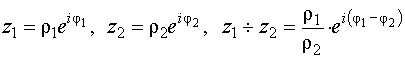 .
.
Модуль частного равен частному модулей делимого и делителя, а аргумент частного равен разности аргументов делимого и делителя.
Если делимое и делитель даны в алгебраической форме, то правило деления таково: для того, чтобы разделить комплексное число (a 1 + b 1 i) на другое комплексное число (a 2 + b 2 i), то есть найти  , нужно и числитель, и знаменатель умножить на число, сопряжённое знаменателю.
, нужно и числитель, и знаменатель умножить на число, сопряжённое знаменателю.
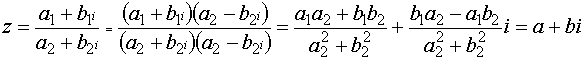 .
.
В результате операции получили элемент того же множества. Значит, операция деления считается введённой.
Возведение в степень комплексных чисел
Операцию возведения в степень удобнее выполнять, когда комплексное число записано в тригонометрической или в показательной форме.
1.  ,
,
2. 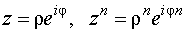 .
.
Для возведения комплексного числа в степень нужно модуль возвысить в эту степень, а аргумент умножить на показатель степени.
Извлечение корня
Определение. Корнем n -ой степени из комплексного числа называется такое комплексное число, n -я степень которого равна подкоренному числу.
Из этого определения следует, что из равенства 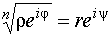 следует равенство
следует равенство  .
.
 Из равенства комплексных чисел следует
Из равенства комплексных чисел следует  , а аргументы отличаются на число, кратное
, а аргументы отличаются на число, кратное  ;
;  . Отсюда
. Отсюда  ,
, 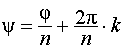 . Здесь
. Здесь  есть арифметическое значение корня, а k – любое целое число. Таким образом, получается формула
есть арифметическое значение корня, а k – любое целое число. Таким образом, получается формула
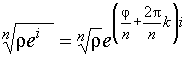 .
.
В этой формуле число k может принимать всевозможные целые значения, но различных значений корня будет только n и они соответствуют значениям k = 0, 1, 2, …, n - 1.
Докажем этот факт. Действительно, правые части в этой формуле различны тогда, когда аргументы 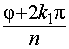 и
и  отличаются на величину, не кратную
отличаются на величину, не кратную  , и будут одинаковыми, если указанные аргументы отличаются на величину, кратную
, и будут одинаковыми, если указанные аргументы отличаются на величину, кратную  . Поэтому разность
. Поэтому разность
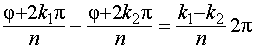
не может быть кратна  . Из этого результата и следует, что любым подряд взятым n целым числам k соответствуют n различных значений корня.
. Из этого результата и следует, что любым подряд взятым n целым числам k соответствуют n различных значений корня.
Пусть теперь k 3– целое число, не входящее в эту последовательность подряд взятых значений k. Это число можно представить в виде k 3= gn + ki, где g – целое число, а ki – одно из чисел этого ряда, поэтому 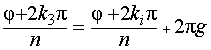 , то есть значению k 3 соответствует то же значение корня, что и значению ki.
, то есть значению k 3 соответствует то же значение корня, что и значению ki.
Вывод: корень n -ой степени из комплексного числа имеет n различных значений. Исключением из этого правила является лишь частный случай, когда извлекается корень из нуля. В этом случае все значения корня равны нулю.
Пример 1. Решить уравнения а) x 2 + 25 = 0, б) x 3 + 27 =0.
Решение. а)  , то есть первое уравнение имеет два мнимых корня: x 1 = 5 i, x 2 = -5 i;
, то есть первое уравнение имеет два мнимых корня: x 1 = 5 i, x 2 = -5 i;
б) воспользуемся формулой x 3 + a 3 = (x + a) (x 2 - ax + a 2), x 3 + 27 = (x +3) (x 2 - 3 x + 9). Приравнивая нулю каждый из множителей, получаем один корень действительный и два комплексных:

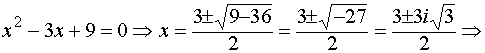
 ;
;
x 2 и x 3 – сопряжённые комплексные числа.
Пример 2. Вычислить, изобразить на плоскости, записать в тригонометрической и показательной форме:
а)  ; б) (i) i.
; б) (i) i.
Решение. а) Сначала запишем числа в алгебраической форме, выполнив
операцию деления. Домножим на сопряжённое число, и, учитывая, что i 2 = -1, получим:
 = - 3 - 3i;
= - 3 - 3i;
х = Re z = - 3, у = Jm z = - 3, что соответствует точке на плоскости (- 3, - 3) (см рис.3).
Модуль комплексного числа:
 .
.
Так как точка находится в третьей четверти, то аргумент комплексного числа будет:
 ,
,
Записываем тригонометрическую и показательную формы комплексного числа:
 .
.
 б) z = i i, i = 0 + 1 · i, х = Re z = 0, у = Jm z = 1,
б) z = i i, i = 0 + 1 · i, х = Re z = 0, у = Jm z = 1,
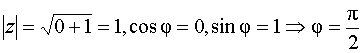 .
.
 – действительное число (точка на оси ох) (см. рис. 4).
– действительное число (точка на оси ох) (см. рис. 4).
Пример 3. Вычислить  .
.
Решение. Представим число в тригонометрической (или показательной) форме, для чего найдём его модуль и аргумент:
- 1 = - 1 + 0 · i, х = - 1, у = 0,
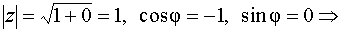
 , k = 0, 1, 2.
, k = 0, 1, 2.
k = 0, 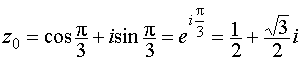 ;
;
k = 1, 
k = 2,  .
.
 Упражнения для самостоятельной работы
Упражнения для самостоятельной работы
Произведите сложение и вычитание комплексных чисел:
14. (3 + 5i) + (7 – 2i).
15. (6 + 2i) + (5 + 3i).
16. (– 2 + 3i) + (7 – 2i).
17. (5 – 4i) + (6 + 2i).
18. (3 – 2i) + (5 + i).
19. (4 + 2i) + (– 3 + 2i).
20. (– 5 + 2i) + (5 + 2i).
21. (– 3 – 5i) + (7 – 2i).
 Произведите умножение комплексных чисел:
Произведите умножение комплексных чисел:
22. (2 + 3 i)(5 – 7i).
23. (6 + 4i)(5 + 2i).
24. (3 – 2i)(7 – i).
25. (– 2 + 3i)(3 + 5i).
26. (1 –i)(1 + i).
27. (3 + 2i)(1 + i).
28. (6 + 4i) Ч 3i.
29. (2 – 3i)(– 5i).
Произведите деление комплексных чисел:

 Решите уравнения:
Решите уравнения:
1) x 2 – 4 x + 13 = 0.
2) x 2 + 3 x + 4 = 0.
3) 2,5 x 2 + x + 1 = 0.
4 4 x 2 – 20 x + 26 = 0.
Список литературы
1. Пехлецкий И. Д. Математика, СПО. - М.: Академия, 2008.
2. Григорьев С.Г., Задулина С.В. Математика, СПО. - М.: Академия, 2009.
3. Спирина М.С., Спирин П.А. Теория вероятностей и математическая статистика, СПО. - М.: Академия, 2007.
4. Валуце И.И., Дилигул Г.Д. Математика для техникумов. - М.: Наука, 1980.
5. Подольский В. А., Суходский А.М. Сборник задач по высшей математике. - М.: Высшая школа, 1974.
6. Башмаков М.И. Математика, 10 кл. - М.: Академия, 2009.
7. Башмаков М.И. Математика, 11 кл. - М.: Академия, 2009.
8. Шибасов Л.П., Шибасова З.Ф. За страницами учебника математики. - М.: Просвещение, 1997
ПРАКТИЧЕСКАЯ РАБОТА №2
«Корни, степени и логарифмы»
Цели урока:
1) Обобщить теоретические знания по теме: «Корни, степени и логарифмы».
2) Рассмотреть алгоритмы решений заданий теме «Корни, степени и логарифмы», решить задачи.
3) Формировать потребность к самопознанию; умение ставить цели и реализовывать их.
Теоретический материал
При выполнении заданий по данной теме вы должны помнить:
1. Определения степени:  где m – целое число, а n – натуральное.
где m – целое число, а n – натуральное.
2. Свойства степени:
1) a0=1;
2)  ;
;
3)  ;
;
4) 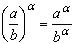 ;
;
5) 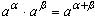 ;
;
6)  ;
;
7)  .
.
3. Определение корня:  .
.
4. Арифметический корень:  .
.
5. Свойства корней:
1) 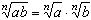 ;
;
2)  ;
;
3) 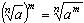 ;
;
4) 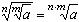 , где m, n – натуральные числа.
, где m, n – натуральные числа.
5)  .
.
6. Формулы сокращённого умножения:
1) (a + b)2 = a2 + 2ab + b2;
2) (a – b)2 = a2 – 2ab + b2;
3) a2 – b2 = (a + b) ∙ (a – b);
4) a3 + b3 = (a + b) ∙ (a2 – ab + b2);
5) a3 – b3 = (a – b) ∙ (a2 + ab + b2);
6) (a + b)3 = a3 + 3a2b + 3ab2 + b3;
7) (a – b)3 = a3 – 3a2b + 3ab2 – b3.
7. Определение логарифма: logab=x  ax=b, a>0, a
ax=b, a>0, a  1, b>0.
1, b>0.
8. Основное логарифмическое тождество: alogab=b.
9. Десятичный логарифм (по основанию 10): lgb:10lgb=b.
10. Натуральный логарифм (по основанию e): lnb:elnb=b.
11. Свойства логарифмов:
1) loga1=0;
2) logaa=1;
3) loga(x∙y)=logax+logay;
4) loga 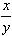 =;logax-logay;
=;logax-logay;
5) logaxp= p∙logax;
6)  – переход к новому основанию;
– переход к новому основанию;
7)  .
.
Базовый уровень
Пример. Вычислить  .
.
Решение:
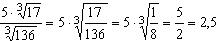 .
.
Ответ: 2,5.
Пример. Вычислить  .
.
Решение:

Ответ: 15.
Пример. Вычислить: 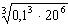 .
.
Решение:
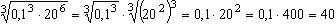 .
.
Ответ: 40.
Пример. Сравнить числа  и
и  .
.
Решение:
Преобразуем данные числа так, чтобы степени корня в них были равны.
 .
.
Делаем вывод, что данные числа равны.
Ответ:  .
.
Пример. Выразите величину р из равенства  .
.
Решение:
 .
.
Ответ:  .
.
Пример. Определите знак разности 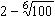 .
.
Решение:
Так как 
Ответ: Разность отрицательна.
Пример. Вычислить 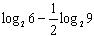 .
.
Решение:
 .
.
Ответ: 1.
Повышенный уровень
Пример. Вычислить  .
.
Решение:
 .
.
Ответ: 2.
Пример. Вычислить  .
.
Решение:

Ответ: 6.
Пример. Вычислить 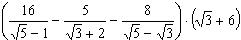 .
.
Решение:
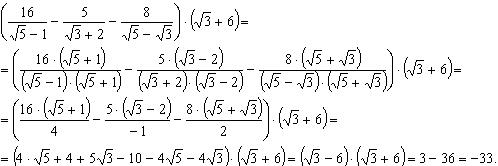
Ответ: – 33.
Пример. Вычислить  .
.
Решение:
 .
.
Ответ: – 10.
Пример. Выделить полный квадрат 3у2 + 6у – 8.
Решение:
3у2 + 6у – 8 = 3(у2 + 2у) – 8 = 3(у2 + 2у + 1) – 3 – 8 = 3(у + 1)2 – 11.
Ответ: 3(у + 1)2 – 11.
Пример. Упростить 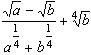 .
.
Решение:
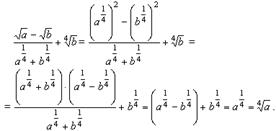 .
.
Ответ:  .
.
Пример. Упростите выражение  и найдите его значение при
и найдите его значение при  .
.
Решение:
 .
.
При  а2 =3.
а2 =3.
Ответ: а2; 3.
Пример. Сократить дробь  .
.
Решение:
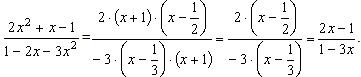
Полезно помнить, что если х1 и х2 – корни квадратного трёхчлена ax2 + bx + c, где а ≠ 0, то его можно разложить на множители: ax2 + bx + c = а(х – х1) ∙ (х – х2).
Ответ:  .
.
Пример. Упростить  если m<0.
если m<0.
Решение:
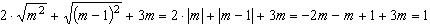 .
.
Ответ: 1.
Пример. Вычислить  , если logba=2.
, если logba=2.
Решение:

Ответ: – 5.
 Упражнения для самостоятельной работы:
Упражнения для самостоятельной работы:
Базовый уровень
1) Вычислите  .
.
2) Вычислите  .
.
3) Вычислить без калькулятора  .
.
4) Найдите значение выражения (10–10 ∙ 1006)–1.
5) Упростите выражение 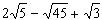 .
.
6) Найдите значение выражения 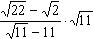 .
.
7) Найдите значение выражения  .
.
8) Вычислите  .
.
9) Упростите выражение  .
.
10) Вычислить  .
.
11) Выполните действия 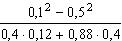 .
.
12) Упростите выражение  .
.
Средний уровень
13) Вычислите  .
.
14) Вычислите  .
.
 Повышенный уровень
Повышенный уровень
15) Вычислите 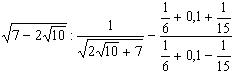 .
.
16) Вычислите 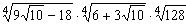 .
.
17) Вычислите  .
.
18) Вычислите  .
.
19) Упростить 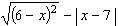 если х > 7.
если х > 7.
20) Упростить  .
.
54) Упростить  .
.
Список литературы
9. Пехлецкий И. Д. Математика, СПО. - М.: Академия, 2008.
10. Григорьев С.Г., Задулина С.В. Математика, СПО. - М.: Академия, 2009.
11. Спирина М.С., Спирин П.А. Теория вероятностей и математическая статистика, СПО. - М.: Академия, 2007.
12. Валуце И.И., Дилигул Г.Д. Математика для техникумов. - М.: Наука, 1980.
13. Подольский В. А., Суходский А.М. Сборник задач по высшей математике. - М.: Высшая школа, 1974.
14. Башмаков М.И. Математика, 10 кл. - М.: Академия, 2009.
15. Башмаков М.И. Математика, 11 кл. - М.: Академия, 2009.
16. Шибасов Л.П., Шибасова З.Ф. За страницами учебника математики. - М.: Просвещение, 1997.
ПРАКТИЧЕСКАЯ РАБОТА № 3
«Основы тригонометрии»
Цели урока:
1) Обобщить теоретические знания по теме: «Основы тригонометрии».
2) Рассмотреть алгоритмы решений заданий теме «Основы тригонометрии», решить задачи.
3) Формировать умение планировать свою деятельность; умение ставить цели и реализовывать их.
Теоретический материал
Основные тригонометрические формулы
Основные формулы тригонометрии
Перевод градусной меры угла в радианную и обратно. Пусть a° - градусная мера угла, b - радианная, тогда справедливы формулы:

| 
|
Формулы зависимости между функциями одного и того же аргумента.
| 1. | 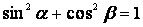
| 4. | 
|
| 2. | 
| 5. | 
|
| 3. | 
| 6. | 
|
Формулы сложения.
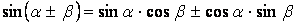
|
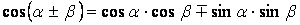
|

|
Формулы двойных и половинных углов.
| 1. | 
| 5. | 
|
| 2. | 
| 6. | 
|
| 3. | 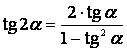
| 7. | 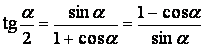
|
| 4. | 
| 8. | 
|
Формулы преобразования суммы в произведение.

|
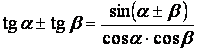
|
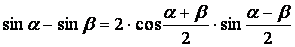
| |

| 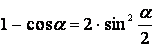
|

| 
|
Формулы преобразования произведения в сумму.
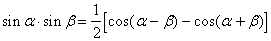
|
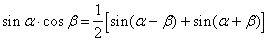
|

|
Формулы приведения.
| j | 
| 
| 
| 
| 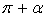
| 
| 
| 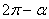
| 
|
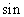 j j
| - 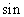 a a
|  a a
|  a a
| 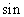 a a
| - 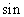 a a
| -  a a
| -  a a
| - 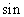 a a
| 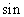 a a
|
 j j
|  a a
| 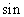 a a
| - 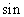 a a
| -  a a
| -  a a
| - 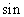 a a
| 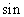 a a
|  a a
|  a a
|
 j j
| -  a a
| 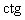 a a
| - 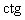 a a
| -  a a
|  a a
| 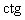 a a
| - 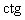 a a
| -  a a
|  a a
|
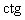 j j
| - 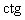 a a
|  a a
| -  a a
| - 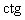 a a
| 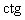 a a
|  a a
| -  a a
| - 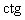 a a
| 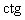 a a
|
Решение простейших тригонометрических уравнений
| Уравнение | Общее решение | Частные случаи | ||

| 
| 
| ||
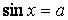 , ,

| 
| 
|

| 
|
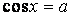 , ,

| 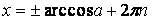
|

| 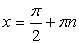
|

|
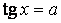 , ,

| 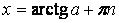
| 
|

| 
|
 , ,

| 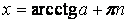
| 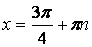
| 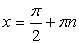
| 
|
Для решения простейших тригонометрических неравенств  ,
,  ,
, 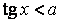 ,
, 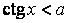 (вместо знака
(вместо знака  могут стоять
могут стоять  ,
, 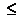 ,
,  ) применяют графический способ. Находят точки пересечения графика соответствующей функции с прямой
) применяют графический способ. Находят точки пересечения графика соответствующей функции с прямой  , расположенные ближе к началу координат, и затем используют периодичность функции.
, расположенные ближе к началу координат, и затем используют периодичность функции.
Для решения более сложных тригонометрических неравенств их сводят к простейшим случаям с помощью упрощений. Графики и основные свойства тригонометрических функций.

|  для для 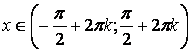
|
 для для 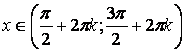
| |
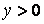 для для 
| |
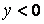 для для 
| |
 , ,  , ,  , период , период  , нечетная , нечетная
| |
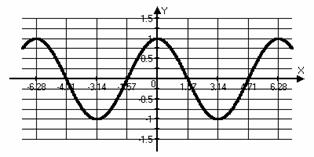
|  для для 
|
 для для 
| |
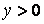 для для 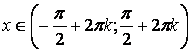
| |
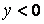 для для 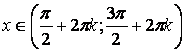
| |
 , ,  , ,  , период , период  , четная , четная
| |

|  для для 
|
 для для 
| |
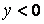 для для 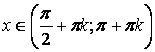
| |
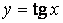 , ,  \ \  , , 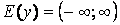 , период , период 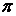 , нечетная , нечетная
| |

|  для для 
|
 для для 
| |
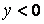 для для 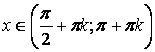
| |
 , ,  \ \  , , 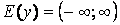 , период , период 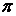 , нечетная , нечетная
|
Графики и основные свойства обратных тригонометрических функций.

|  для для 
|
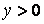 для для 
| |
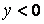 для для 
| |
| Функция нечетная | |
 , ,  , , 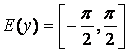 , непериодическая функция , непериодическая функция
| |
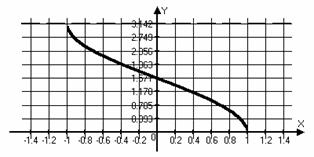
|  для для 
|
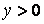 для для 
| |
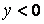 для для 
| |
| Функция ни четная, ни нечетная | |
 , ,  , ,  , непериодическая функция , непериодическая функция
| |

|  для для 
|
 для для 
| |
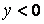 для для 
| |
| Функция нечетная | |
 , ,  , ,  , непериодическая функция , непериодическая функция
| |
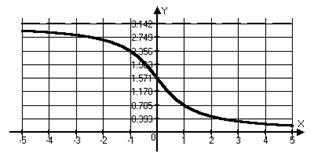
|  для для 
|
 для для 
| |
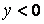 для для 
| |
| Функция ни четная, ни нечетная | |
 , ,  , , 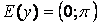 , непериодическая функция , непериодическая функция
|
Примеры решения задач.
1.  Найти значение следующих тригонометрических выражений:
Найти значение следующих тригонометрических выражений:
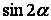 ,
, 
 , если
, если  .
.
Решение. Выпишем формулы для нахождения 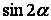 ,
, 
 :
:
 ,
,  ,
, 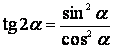 .
.
 .
.
Из основного тригонометрического тождества найдем 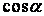 :
:
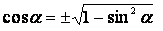

Далее найдем значения искомых выражений:

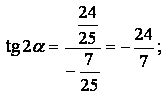
Ответ:  ,
, 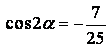 ,
, 
2.  Доказать тождество:
Доказать тождество:
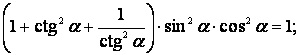
Решение. Приведем левую часть к 1:

 .
.
Тождество доказано.
3.  Вычислить значение выражения:
Вычислить значение выражения:

Решение. Используя формулы приведения, получим:


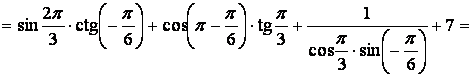

Итак, значение выражения 0.
 Пояснения к разделу: Решение тригонометрических уравнений и неравенств.
Пояснения к разделу: Решение тригонометрических уравнений и неравенств.
Для решения произвольных тригонометрических уравнений и неравенств применяют те же основные приемы, которые были описаны ранее для решения алгебраических уравнений: введение новой переменной и разложение на множители левой части уравнения или неравенства.
1. Уравнения, однородные относительно  и
и 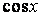 .
.
Каждое из уравнений:
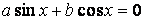 ,
,
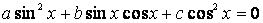 и т.д.
и т.д.
называется однородным относительно  и
и 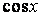 . Сумма показателей степеней у
. Сумма показателей степеней у  и
и 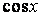 во всех членах такого уравнения одинакова. Эта сумма называется степенью однородного уравнения. Делением на
во всех членах такого уравнения одинакова. Эта сумма называется степенью однородного уравнения. Делением на 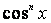 ,
,  степень однородного уравнения, оно приводится к уравнению, алгебраическому относительно
степень однородного уравнения, оно приводится к уравнению, алгебраическому относительно  .
.
Разделив, например, уравнение 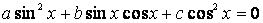 на
на 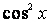 , получим уравнение:
, получим уравнение:
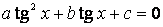 .
.
При  эти уравнения эквивалентны, так как если
эти уравнения эквивалентны, так как если 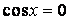 , то из первого уравнения получим, что и
, то из первого уравнения получим, что и  , что невозможно (
, что невозможно (  и
и 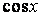 при одном и том же аргументе в нуль не обращаются). Далее из эквивалентного уравнения находим
при одном и том же аргументе в нуль не обращаются). Далее из эквивалентного уравнения находим  , решая квадратное уравнение относительно
, решая квадратное уравнение относительно  , а по значениям
, а по значениям  - соответствующие значения
- соответствующие значения  .
.
4.  Решить уравнение:
Решить уравнение:
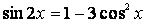
Решение. Заменяя  и
и  , получим однородное уравнение:
, получим однородное уравнение:  ,
,
Или  .
.
Деля на 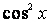 (
(  ), получим:
), получим:
 .
.
Вводим новую переменную 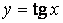 и получаем квадратное уравнение относительно нее:
и получаем квадратное уравнение относительно нее:
 .
.
Корни этого уравнения:  . Далее получаем равносильную совокупность уравнений:
. Далее получаем равносильную совокупность уравнений:


 2. Уравнения, левая часть которых раскладывается на множители, а правая часть равна нулю.
2. Уравнения, левая часть которых раскладывается на множители, а правая часть равна нулю.
Перенеся все члены любого уравнения в левую часть, его можно привести к виду  .
.
Если левая часть этого уравнения раскладывается на сомножители, то каждый из них приравнивается к нулю, и уравнение распадается на несколько простых уравнений. Очень важно при этом иметь в виду, что корнями первоначального уравнения будут только те из корней полученных уравнений, которые входят в область определения первоначального уравнения.
5.  Решить уравнение:
Решить уравнение:
 .
.
Решение. Здесь целесообразно использовать формулы преобразования произведения тригонометрических функций в сумму. Воспользовавшись этими формулами, получим уравнение:

или 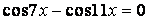 .
.
Разность косинусов преобразуем в произведение  , которое равносильно совокупности уравнений:
, которое равносильно совокупности уравнений:

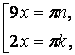
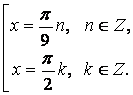
 3. Уравнения вида
3. Уравнения вида  .
.
Эти уравнения можно решать при помощи универсальной тригонометрической подстановки  , воспользовавшись формулами, выражающими
, воспользовавшись формулами, выражающими  и
и 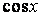 через
через  :
:
 и
и 






