
 1)
1) 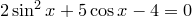 ,
,
2) 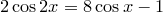 ,
,
 3)
3) 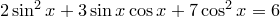 ,
,
 4)
4) 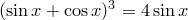 ,
,
 5)
5) 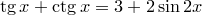 ,
,
 6)
6) 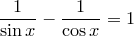 ,
,
 7)
7) 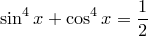 .
.
8) Решите уравнения
 9)
9) 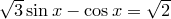 ,
,
 10)
10) 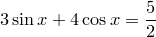 .
.


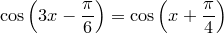 ,
,
11ч) 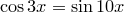 ,
,
Решите тригонометрические неравенства
 12)
12) 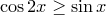 ,
,
 13)
13) 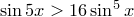 ,
,
 14)
14) 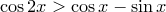 ,
,
 15)
15) 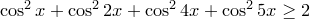 .
.
Список литературы
17.Пехлецкий И. Д. Математика, СПО. - М.: Академия, 2008.
18. Григорьев С.Г., Задулина С.В. Математика, СПО. - М.: Академия, 2009.
19. Спирина М.С., Спирин П.А. Теория вероятностей и математическая статистика, СПО. - М.: Академия, 2007.
20. Валуце И.И., Дилигул Г.Д. Математика для техникумов. - М.: Наука, 1980.
21. Подольский В. А., Суходский А.М. Сборник задач по высшей математике. - М.: Высшая школа, 1974.
22. Башмаков М.И. Математика, 10 кл. - М.: Академия, 2009.
23. Башмаков М.И. Математика, 11 кл. - М.: Академия, 2009.
24. Шибасов Л.П., Шибасова З.Ф. За страницами учебника математики. - М.: Просвещение, 1997.
ПРАКТИЧЕСКАЯ РАБОТА № 4
«Функции, их свойства и графики»
Цели урока:
1) Обобщить теоретические знания по теме: «Функции, свойства и графики».
2) Рассмотреть алгоритмы решений заданий теме «Функции, свойства и графики», решить задачи.
3) Формировать умение самоконтроля, рассудительность, терпение, самостоятельность.
Теоретический материал
График линейной функции
Линейная функция задается уравнением 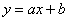 . График линейной функций представляет собой прямую. Для того, чтобы построить прямую достаточно знать две точки.
. График линейной функций представляет собой прямую. Для того, чтобы построить прямую достаточно знать две точки.
Пример 1
Построить график функции 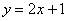 . Найдем две точки. В качестве одной из точек выгодно выбрать ноль.
. Найдем две точки. В качестве одной из точек выгодно выбрать ноль.
Если 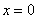 , то
, то 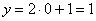
Берем еще какую-нибудь точку, например, 1.
Если 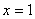 , то
, то 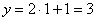
При оформлении заданий координаты точек обычно сводятся в таблицу:
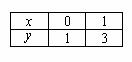
А сами значения рассчитываются устно или на черновике, калькуляторе.
Две точки найдены, выполним чертеж:

При оформлении чертежа всегда подписываем графики.
Не лишним будет вспомнить частные случаи линейной функции:

График квадратичной, кубической функции
Парабола. График квадратичной функции 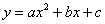 (
(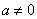 ) представляет собой параболу. Рассмотрим канонический случай:
) представляет собой параболу. Рассмотрим канонический случай: 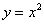

Пример 2
Построить график функции 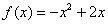 .
.
В этом примере мы рассмотрим важный технический вопрос: Как быстро построить параболу? В практических заданиях необходимость начертить параболу возникает очень часто, в частности, при вычислении площади фигуры с помощью определенного интеграла. Поэтому чертеж желательно научиться выполнять быстро, с минимальной потерей времени. следующий алгоритм построения.
Сначала находим вершину параболы. Для этого берём первую производную и приравниваем ее к нулю:
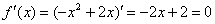
Если с каком порядке находить остальные точки, думаю, будет понятно из итоговой таблицы:

Выполним чертеж:

Из рассмотренных графиков вспоминается еще один полезный признак:
Для квадратичной функции 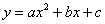 (
(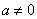 ) справедливо следующее:
) справедливо следующее:
Если, то ветви параболы направлены вверх.
Если, то ветви параболы направлены вниз.
Кубическая парабола






