Пусть производственная фирма выпускает один вид продукции или много видов, но в постоянной структуре. Тогда годовой выпуск фирмы в натурально-вещественной форме X - это число единиц продукции одного вида или число многономенклатурных агрегатов.
Для производства продукции фирма использует настоящий труд L (среднее число занятых в год либо отработанные за год человеко-часы) и прошлый труд в виде средств труда К (основные производственные фонды) и предметов труда М (затраченные за год топливо, энергия, сырье, материалы, комплектующие и т.п.). Каждый из этих трех агрегированных видов ресурсов (труд, фонды и материалы) имеет определенное число разновидностей (труд разной квалификации, оборудование различного вида и т.п.). Обозначим вектор-столбец возможных объемов затрат различных видов ресурсов через 
. Тогда технология фирмы определяется ее производственной функцией, выражающей связь между затратами ресурсов и выпуском:
(23.1)
Предполагается, что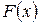 
является дважды непрерывно-дифференцируемой и неоклассической, кроме того, ее матрица вторых производных отрицательно определена.
Если цена единицы продукции равна р, а цена единицы ресурса j -го вида – 
, то каждому вектору затрат х отвечает прибыль
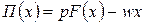, (23.2)
где 
– вектор-строка цен ресурсов.
Цены ресурсов имеют естественный и понятный смысл: если 
— среднегодовое число занятых определенной профессии, то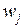 
– годовая заработная плата одного работника данной профессии; если — покупные материалы (топливо, энергия и т.п.), то 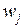– покупная цена единицы данного материала; если – производственные фонды определенного вида, то 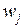– годовая арендная плата за единицу фондов или стоимость поддержания единицы фондов в исправности, если фирма владеет этими средствами.
В (23.2) 
— стоимость годового выпуска фирмы или ее годовой доход,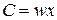 
– издержки производства или стоимость затрат ресурсов за год.
Если нет других ограничений на размеры вовлекаемых в производство ресурсов, кроме естественного требования их неотрицательности, то задача на максимум прибыли приобретает вид
. (23.3)
Это задача нелинейного программирования с п условиями неотрицательности 
, необходимыми условиями ее решения являются условия Куна—Таккера.
(23.4)
Если в оптимальном решении использованы все виды ресурсов, т.е. 
, то условия (23.4) принимают вид
(23.5)
или
т.е. в оптимальной точке стоимость предельного продукта данного ресурса должна равняться его цене.
Точно такое же по форме решение имеет задача на максимум выпуска при заданном объеме издержек
(23.6)
Это задача нелинейного программирования с одним линейным ограничением и условием неотрицательности переменных. Согласно теории вначале строим функцию Лагранжа
,
затем максимизируем ее при условии неотрицательности переменных. Для этого необходимо выполнение условий Куна—Таккера
(23.7)
Как видим, условия (23.7) полностью совпадают с (23.4), если 
.
Пример 1. Выпуск однопродуктовой фирмы задается следующей производственной функцией Кобба-Дугласа:
.
Определить максимальный выпуск, если на аренду фондов и оплату труда выделено 150 д.е., стоимость аренды единицы фондов 
, ставка заработной платы 
.
Какова предельная норма замены одного занятого фондами в оптимальной точке?
Решение. Поскольку 
, то в оптимальном решении 
, 
, поэтому условия (23.7) принимают вид
(23.8)
или в нашем случае
Поделив первое уравнение на второе, получаем
Подставив это соотношение в условие 
, находим
Решение можно проиллюстрировать геометрически. На рис. 23.1 изображены изокосты (линии постоянных издержек для С= 50, 100, 150) и изокванты (линии постоянных выпусков для X =25,2; 37,8).
Рисунок - 23.1
Изокосты имеют следующие уравнения: 
.
Изокванты имеют следующие уравнения: 
.
В оптимальной точке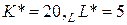 
изокванта X* = 37,8 и изокоста С= 150, проходящие через эту точку, касаются, поскольку согласно (23.8) нормали к этим кривым, заданные градиентами 
, 
, коллинеарны.
Норма замены труда фондами в оптимальной точке
т.е. один работающий может быть заменен двумя единицами фондов. Решая задачу фирмы (23.3) на максимум прибыли, находим единственный оптимальный набор ресурсов (рассматриваем случай, когда все ресурсы войдут в набор). Этому набору отвечает единственное значение издержек 
. Решим теперь задачу (23.6) на максимум выпуска при заданных издержках 
. Если 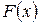— неоклассическая производственная функция, то в оптимальном решении , причем это решение единственно. Таким образом, с одной стороны,
а с другой стороны –
Поскольку 
и 
, то 
, но 
, поэтому 
. Так как решение задачи (23.3) единственно, то 
.
Итак, если задача на максимум прибыли имеет единственное решение , то ей отвечает задача на максимум выпуска при заданных издержках , причем последняя имеет такое же решение, как и первая (см. рис. 23.1).
Геометрическое место точек касания изокост и изоквант при разных значениях издержек С определяет долгосрочный путь развития фирмы 
, т.е. показывает, как будет увеличиваться (уменьшаться) выпуск, если издержки возрастут (уменьшатся). Поскольку эта зависимость монотонна, то существует обратная монотонная функция издержек
.
Поскольку – максимальный выпуск при заданных издержках С, то издержки 
, отвечающие этому максимальному выпуску X, - минимальные издержки.
Если известна функция минимальных издержек С(X), оптимальный размер выпуска снова определяется из условия максимума прибыли
(23.9)
Приравниваем к нулю производную:
т.е. в оптимальной точке предельные издержки равны цене выпуска:
(кроме того, максимум прибыли достигается при 
).
Рассмотрим п соотношений (23.5)
Эти соотношения могут быть разрешены относительно х в окрестности оптимальной точки, если якобиан 
, где
Это означает, что должен быть отличен от нуля гессиан |Н| производственной функции (но Н отрицательно определена, поэтому действительно 
). Тогда
(23.10)
или
Эти п уравнений задают функции спроса (на ресурсы), найденные с помощью модели поведения фирмы. Функции спроса на ресурсы могут быть также найдены экспериментально с помощью методов математической статистики по выборочным данным. Функция предложения
.
