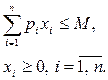Одним из важных понятий экономической теории является домашнее хозяйство (потребитель). Главная проблема при изучении поведения потребителя заключается в том, чтобы установить, в каких объемах он приобретет наличные товары и услуги при заданных ценах и доходе.
Конкретное решение потребителя о покупке определенного набора товаров математически можно представить как выбор конкретной точки в пространстве товаров. Пусть 
– конечное число рассматриваемых товаров, а 
– вектор-столбец товаров, приобретенных потребителем за определенный срок (например, за год) при заданных ценах и доходе за тот же срок. Данный вектор называют потребительским набором.
Пространство товаров – это множество всевозможных наборов товаров 
с неотрицательными координатами
В теории потребительского выбора предполагается, что каждый потребитель изначально имеет свои предпочтения на некотором подмножестве пространства товаров 
. Это означает, что для каждой пары 
, 
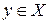имеет место одно из трех отношений:
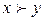– набор х предпочтительнее у;
– набор х менее предпочтителен, чем у;
~ 
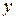– для потребителя оба набора обладают одинаковой степенью предпочтения.
Отношения предпочтения обладают по крайней мере следующими свойствами:
1) если ,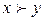 
, то 
(транзитивность);
2) если 
, то 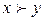(ненасыщаемость: больший набор всегда предпочтительнее меньшего).
Отношения предпочтения каждого потребителя при определенных слабых предположениях, касающихся предпочтений, можно (и удобно!) представить в форме индикатора предпочтений, т.е. такой функции полезности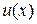 
, что из 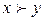следует 
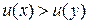и из ~ 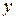следует 
. Для каждого потребителя такое представление многовариантно. Например, если 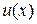– функция полезности, то 
, 
– это также индикаторы предпочтений.
Введение функции полезности позволяет заменить отношения предпочтения привычными отношениями между числами: больше, меньше, равно.
В теории потребления предполагается, что функция полезности обладает следующими свойствами:
1) 
– с ростом потребления блага полезность растет;
2) 
– небольшой прирост блага при его первоначальном отсутствии резко увеличивает полезность;
3) 
– с ростом потребления блага скорость роста полезности замедляется;
4) 
– при очень большом объеме блага его дальнейшее увеличение не приводит к увеличению полезности.
Условие 3 обычно используется в более расширительной трактовке: матрица вторых производных (матрица Гессе)
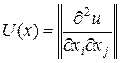
отрицательно определена.
Предельной полезностью товара называется предел отношения приращения полезности к вызвавшему этот прирост приращению товара:
таким образом, предельная полезность показывает, насколько возрастет полезность, если товар возрастет на малую единицу.
Поверхностью безразличия называется гиперповерхность размера 
, на которой полезность постоянна:
или в дифференциальной форме
(22.1)
Условие (22.1) означает, что касательная к поверхности безразличия перпендикулярна градиенту полезности.
С точки зрения потребителя наличие множества наборов товаров, обладающих одинаковой полезностью (т.е. одинаковой степенью предпочтения), означает возможность замены одного набора другим равноценным набором, в том числе возможность замены одного товара другим.
Пусть в соотношении (22.1)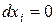 
для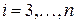 
, тогда это соотношение примет вид
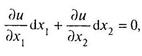
Откуда 
(22.2)
т.е. предельная норма замены первого товара вторым равна отношению предельных полезностей первого и второго товаров. Норма замены показывает, сколько требуется единиц второго товара, чтобы заменить выбывшую малую единицу первого товара.
Задача потребительского выбора (задача рационального поведения потребителя на рынке) заключается в выборе такого потребительского набора , который максимизирует его функцию полезности при заданном бюджетном ограничении.
Бюджетным множеством называется множество тех наборов товаров, которые может приобрести потребитель, имея доход 
:
,
где 
– вектор-строка цен.
Формально задача потребительского выбора имеет вид:
u (x) ® max (22.3)
при условиях
