Пусть рассматривается функция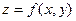 
, аргументы x и y которой удовлетворяют условию 
, называемому уравнением связи.
Определение
Точка 
называется точкой условного максимума (минимума), если существует такая окрестность этой точки, что для всех точек (x,y) из этой окрестности удовлетворяющих условию , выполняется неравенство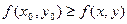 
.
Точка условного максимума (минимума) не является точкой безусловного экстремума.
Наиболее простым способом нахождения условного экстремума функции двух переменных является сведение задачи к отысканию экстремума функции одной переменной. Допустим уравнение связи удалось разрешить относительно одной из переменных, например, выразить y через x: 
. Подставив полученное выражение в функцию двух переменных, получим 
, то есть функцию одной переменной. Ее экстремум и будет условным экстремумом функции .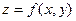
Пример
Найти точки максимума и минимума функции 
при условии 
.
Решение
Выразим из уравнения переменную y через переменную x и подставим полученное выражение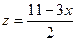 
в функцию z. Получаем 
. Эта функция имеет единственный минимум при x 0=3. Соответствующее значение функции 
. Таким образом, (3, 1) – точка условного экстремума.
В рассмотренном примере уравнение связи оказалось линейным, поэтому его легко удалось разрешить относительно одной из переменных. Однако в более сложных случаях сделать это не удается.
Для отыскания условного экстремума в общем случае используется метод неопределенных множителей Лагранжа.
Рассмотрим функцию трех переменных 
.
Эта функция называется функцией Лагранжа, а l – множителем Лагранжа.
Теорема
Если точка является точкой условного экстремума функции 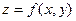при условии , то существует значение l 0 такое, что точка 
является точкой экстремума функции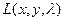 
.
Таким образом, для нахождения условного экстремума функции 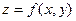при условии требуется найти решение системы
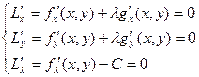
Последнее из этих уравнений совпадает с уравнением связи.
Пример
Найти точки экстремума функции при условии , используя метод множителей Лагранжа.
Решение
Составляем функцию Лагранжа 
. Приравняем к нулю ее частные производные, получим систему уравнений
Ее единственное решение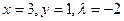 
. Таким образом, точкой условного экстремума может быть только точка (3,1). Нетрудно убедиться, что в этой точке функция 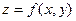имеет условный минимум.
Упражнения
Найти частные производные следующих функций:
| 1. | 
| 2. | 
|
| 3. | 
| 4. | 
|
Найти полные дифференциалы от следующих функций:
| 5. | 
| 6. | 
|
| 7. | 
| 8. |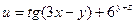 
|
Вычислить частные производные второго порядка:
| 9. | 
| 10. | 
|
