Первая производная функции 
сама является функцией, которая также может иметь производную.
Определение
Производной n–го порядка называется производная от производной (n–1)–го порядка.
Обозначение производных: 
– второго порядка (или вторая производная), 
– третьего порядка (или третья производная).
Для обозначения производных более высокого порядка используются арабские цифры в скобках или римские цифры, например, 
или 
и т.д.
5.6. Основные теоремы дифференциального исчисления – теоремы Ферма, Ролля, Лагранжа
Теорема
Ферма. Пусть функция 
определена на интервале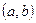 
и имеет наибольшее (наименьшее) значение в точке 
. Тогда, если в точке 
существует производная этой функции, то она равна нулю, т.е. 
.
Геометрический смысл теоремы Ферма: если в точке дифференцируемая функция принимает наибольшее (наименьшее) значение, то в точке 
касательная к графику этой функции параллельна оси 
(Рис. 5.6.1).
Рис. 5.6.1
Заметим, что Теорема неверна, если функция рассматривается на отрезке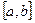 
: в этом случае она может принимать наибольшее и ли наименьшее значение на концах отрезка, где производная не равна нулю.
Теорема (Ролля)
Пусть функция непрерывна на отрезке 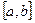и дифференцируема на интервале 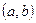, причем 
. Тогда существует точка 
, в которой 
.
Геометрический смысл теоремы Ролля: если функция, непрерывная на отрезке и дифференцируемая внутри ее, на концах этого отрезка принимает одинаковые значения, то хотя бы в одной внутренней точке этого отрезка касательная к графику функции параллельна оси (Рис. 5.6.2).
Рис. 5.6.2
Теорема (Лагранжа)
Пусть функция непрерывна на отрезке 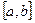и дифференцируема на интервале 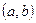. Тогда существует такая точка , что справедлива формула
 .
| (5.6.1) |
Теорема Лагранжа имеет геометрический смысл (рис. 5.6.3). Секущая, проходящая через точки 
и 
, имеет угловой коэффициент, равный 
, а 
– угловой коэффициент касательной к графику функции в точке 
. Теорема Лагранжа утверждает, что существует хотя бы одна точка интервала 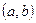, где касательная к графику функции параллельна секущей 
. Приведенные теоремы позволяют сформулировать и обосновать теоремы Лопиталя для раскрытия неопределенностей.
Правило Лопиталя
Определение
Будем говорить, что отношение двух функций 
при 
есть неопределенность вида 
, если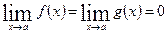 
.
Рис. 5.6.3
Раскрыть эту неопределенность означает вычислить предел 
, если он существует.
Теорема (Лопиталя)
Пусть функции 
и 
определены и дифференцируемы в некоторой окрестности точки 
, за исключением, быть может, самой точки . Кроме того, пусть также 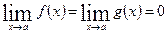, причем 
в указанной окрестности точки . Тогда если существует предел отношения Ошибка! Объект не может быть создан из кодов полей редактирования. (конечный или бесконечный), существует и предел , причем справедлива формула:
 .
| (5.7.1) |
Эту теорему обычно называют правилом Лопиталя.
Замечание 1
Правило Лопиталя можно применить повторно, если 
и 
удовлетворяют тем же требованиям, что и исходные функции и .
Замечание 2
Теорема остается верной и в случае, когда 
(
).
Пример
Здесь мы дважды последовательно применили правило Лопиталя, поскольку два раза имели дело с неопределенностью вида .
Неопределенность вида 
Определение
Будем называть отношение двух функций при неопределенностью вида , если 
, 
или 
. В этом случае правило Лопиталя остается справедливым при замене условия 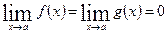на условие .
Пример
Другие виды неопределенностей
Неопределенности вида 
и 
можно свести к неопределенностям вида и с помощью несложных алгебраических преобразований.
Пример
Найти предел 
.
Решение
Здесь имеем неопределенность вида . Преобразуем функцию под знаком предела: 
, в результате имеем неопределенность вида при 
. Теперь, применяя правило Лопиталя, получаем 
.
Неопределенности вида 
, имеющие место при рассмотрении пределов функций 
, сводятся к неопределенностям вида 
с помощью тождественного преобразования
Пример
Найти предел 
.
Решение
Это неопределенность вида 
; используя предыдущую формулу, имеем с учетом только что решенного примера 
.
