Пусть функция y=f(x) дифференцируема в точке  , тогда согласно (5.1.4) Лекции 14 приращение
, тогда согласно (5.1.4) Лекции 14 приращение  в этой точке может быть представлено в виде
в этой точке может быть представлено в виде
 . .
| (5.13.1) |
Первое слагаемое правой части приведенной формулы является бесконечно малой первого порядка, а второе слагаемое – бесконечно малой более высокого порядка, иными словами, величина  является главной частью приращения
является главной частью приращения  , обусловленного приращением аргумента
, обусловленного приращением аргумента  .
.
Определение
Дифференциалом функции y=f(x) в точке 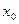 называется главная линейная часть приращения функции в этой точке:
называется главная линейная часть приращения функции в этой точке:  .
.
Поскольку 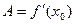 , то эту формулу можно переписать в виде
, то эту формулу можно переписать в виде
 . .
| (5.13.2) |
Таким образом, дифференциалом dx независимой переменной x будем называть приращение этой переменной  , т.е. соотношение (5.13.2) принимает вид
, т.е. соотношение (5.13.2) принимает вид
 . .
| (5.13.3) |
Из равенства (5.13.3) производную f’(x) в любой точке x можно вычислить как отношение дифференциала dy к дифференциалу независимой переменной dx:
 . .
| (5.13.4) |
Тогда равенство (5.13.1) можно переписать в виде
 , ,
| (5.13.5) |
что полностью соответствует определению дифференциала функции.
Пример
Найти приращение и дифференциал функции 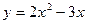 в точке x= 10 и
в точке x= 10 и  .
.
Решение
Приращение функции есть
 .
.
Дифференциал функции – dy=f’(x)dx=( 4 x- 3 )dx. При x= 10,  имеем
имеем  3,72 и dy= 3,70. Различие между ними составляет всего 0,02 или 0,5%.
3,72 и dy= 3,70. Различие между ними составляет всего 0,02 или 0,5%.
Дифференциал функции имеет четкий геометрический смысл (рис 5.13.1).
Пусть точка M на графике функции y=f(x) соответствует значению аргумента 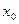 , точка N – значению аргумента
, точка N – значению аргумента  , MS – касательная к кривой y=f(x) в точке M,
, MS – касательная к кривой y=f(x) в точке M, 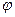 – угол между касательной и осью Ox. Тогда MA – приращение аргумента, AN – соответствующее приращение функции. Рассматривая треугольник ABM, получаем
– угол между касательной и осью Ox. Тогда MA – приращение аргумента, AN – соответствующее приращение функции. Рассматривая треугольник ABM, получаем  , т.е. это главная по порядку величины
, т.е. это главная по порядку величины  и линейная относительно нее часть приращения функции
и линейная относительно нее часть приращения функции  . Второе слагаемое в уравнении (5.13.5) более высокого порядка малости соответствует отрезку BN.
. Второе слагаемое в уравнении (5.13.5) более высокого порядка малости соответствует отрезку BN.

Рис. 5.13.1
Свойства дифференциала
Свойства дифференциала в основном аналогичны свойствам производной.
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5.  .
.
Докажем инвариантность формы первого дифференциала, т.е. универсальность и применимость этой формулы в том случае, когда аргумент x сам является функцией другой переменной t.
Пусть функция y=f(x) дифференцируема в точке x, а сам аргумент x является дифференцируемой функцией аргумента t, т.е.  . Тогда Ошибка! Объект не может быть создан из кодов полей редактирования. сложная функция аргумента t. В силу теоремы о производной сложной функции
. Тогда Ошибка! Объект не может быть создан из кодов полей редактирования. сложная функция аргумента t. В силу теоремы о производной сложной функции  . Поскольку t является независимой переменной, то по форме (5.13.3) записи дифференциала для функции y получаем
. Поскольку t является независимой переменной, то по форме (5.13.3) записи дифференциала для функции y получаем

| (5.13.6) |
Аналогично для дифференциала функции  имеем
имеем  . Подставляя это выражение в формулу (5.13.6) получаем
. Подставляя это выражение в формулу (5.13.6) получаем  , что и требовалось доказать.
, что и требовалось доказать.
Упражнения
Найти производные функций, пользуясь непосредственно определением производной:
| 1. | 
| 2. | 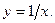
|
| 3. | 
| 4. | 
|
| 5. | 
| 6. | 
|
Определить тангенсы углов наклона касательных к кривым:
| 7. | 
| 8. | 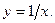
|
| 9. | 
| 10. | 
|
Найти производные функций:
| 11. | 
| 12. | 
|
| 13. | 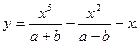
| 14. | 
|
| 15. | 
| 16. | 
|
| 17. | 
| 18. | 
|
| 19. | 
| 20. | 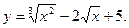
|
| 21. | 
| 22. | 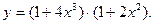
|
| 23. | 
| 24. | 
|
| 25. | 
| 26. | 
|
| 27. | 
| 28. | 
|
| 29. | 
| 30. | 
|
| 31. | 
| 32. | 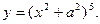
|
| 33. | 
| 34. | 
|
| 35. | 
| 36. | 
|
| 37. | 
| 38. | 
|
| 39. | 
| 40. | 
|
| 41. | 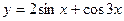
| 42. | 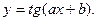
|
| 43. | 
| 44. | 
|
| 45. | 
| 46. | 
|
| 47. | 
| 48. | 
|
| 49. | 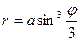
| 50. | 
|
| 51. | 
| 52. | 
|
| 53. | 
| 54. | 
|
| 55. | 
| 56. | 
|
| 57. | 
| 58. | 
|
| 59. | 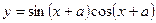
| 60. | 
|
| 61. | 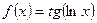
| 62. | 
|
| 63. |  
| 64. | 
|
| 65. | 
| 66. | 
|
| 67. | 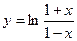
| 68. | 
|
| 69. | 
| 70. | 
|
| 71. | 
| 72. | 
|
| 73. | 
| 74. | 
|
| 75. | 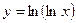
| 76. | 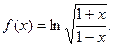
|
| 77. | 
| 78. | 
|
| 79. | 
| 80. | 
|
| 81. | 
| 82. | 
|
| 83. | 
| 84. | 
|
| 85. |  . .
| 86. |  
|
| 87. | 
| 88. | 
|
| 89. | 
| 90. | 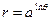
|
| 91. | 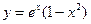
| 92. | 
|
| 93. | 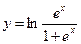
| 94. | 
|
| 95. | 
| 96. | 
|
| 97. | 
| 98. | 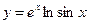
|
| 99. | 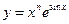
| 100. | 
|
| 101. | 
| 102. | 
|
| 103. | 
| 104. | 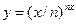
|
| 105. | 
| 106. | 
|
| 107. | 
| 108. | 
|
| 109. | 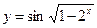
| 110. | 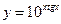
|
Найти производные функций, предварительно логарифмируя эти функции:
| 111. | 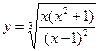
| 112. | 
|
| 113. | 
| 114. | 
|
Дифференцирование неявных функций
Найти dy/dx,
| 115. | 
| 116. | 
|
| 117. | 
| 118. | 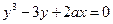
|
| 119. | 
| 120. | 
|
| 121. | 
| 122. | 
|
| 123. | 
| 124. | 
|
Вычислить следующие пределы:
| 125. | 
| 126. | 
|
| 127. | 
| 128. | 
|
Найти экстремумы функций:
| 129. | 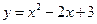
| 130. |  
|
| 131. | 
| 132. | 
|
Найти асимптоты следующих кривых:
| 133. | 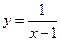
| 134. | 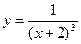
|
| 135. | 
| 136. | 
|






