Пусть функция 
определена на некотором промежутке Х. Придадим значению аргумента в точке 
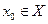произвольное приращение 
так, чтобы точка 
также принадлежала Х. Тогда соответствующее приращение функции составит 
.
Определение
Производной функции в точке 
называется предел отношения приращения функции в этой точке к приращению аргумента при 
(если этот предел существует).
Для обозначения производной функции применяются следующие символы 
или 
:
| (5.1.1) |
Если в некоторой точке предел (5.1.1) бесконечен: 
или 
,
то говорят, что в точке функция имеет бесконечную производную. Если функция имеет производную в каждой точке множества Х, то производная 
также является функцией от аргумента 
, определенной на Х.
Геометрический смысл производной
Для выяснения геометрического смысла производной нам понадобится определение касательной к графику функции в данной точке.
Определение
Касательной к графику функции 
в точке 
называется предельное положение секущей 
, когда точка 
стремится кточке по кривой .
Пусть точка на кривой соответствует значению аргумента , а точка – значению аргумента (Рис. 5.1.1). Из определения касательной следует, что для ее существования в точке нужно, чтобы существовал предел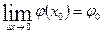 
, который равен углу наклона касательной к оси 
. Из треугольника 
следует, что 
.
Если производная функции в точке существует, то, согласно определению производной (5.1.1), получаем
| (5.1.2) |
Рис. 5.1.1.
Отсюда следует вывод о геометрическом смысле производной: производная в точке равна угловому коэффициенту (тангенсу угла наклона к положительному направлению оси ) касательной к графику функции в точке 
. При этом угол наклона касательной определяется из формулы (5.1.2): 
Правая и левая производные
Определение
Правой (левой) производной функции в точке называется правый (левый) предел отношения (5.1.1) при , если этот предел существует.
Для обозначения односторонних производных используется следующая символика
 ,  .
| (5.1.3) |
Приведем пример функции, у которой существуют, но не равны друг другу, правая и левая производные. Это 
. Действительно, в точке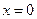 
: 
и 
, т.е. функция не имеет производной при .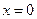
Зависимость между непрерывностью и дифференцируемостью функции
Определение
Функция называется дифференцируемой в точке , если ее приращение 
в этой точке можно представить в виде
 ,
| (5.1.4) |
где 
– некоторое число, не зависящее от , а 
-- бесконечно малая функция при .
Так как произведение двух бесконечно малых функций 
есть бесконечно малая более высокого порядка малости, то формулу можно представить в виде:
 ,
| (5.1.5) |
Теорема
Для того, чтобы функция была дифференцируемой в точке , необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Данная Теорема позволяет в дальнейшем отождествлять дифференцируемость и существование производной для функции одной переменной. Операцию нахождения производной обычно называют дифференцированием.
Если функция имеет производную в каждой точке некоторого промежутка, то говорят, что она дифференцируема на этом промежутке.
Теорема
Если функция дифференцируема в точке , то она и непрерывна в этой точке.
Обратное утверждение не верно: функция , непрерывная в точке, может не иметь производную в этой точке. Например, функция непрерывна в точке 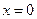, но не имеет производной в этой точке. Таким образом, требование дифференцируемости более сильное, чем требование непрерывности, поскольку из первого вытекает второе.
