Теорема
Если функция f(x) дифференцируема и 
на интервале (a,b), то она не убывает (не возрастает) на этом интервале.
Экстремум функции
Определение
Точка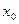 
называется точкой локального максимума (минимума) функции f(x), если для любого числа 
в некоторой окрестности точки 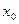выполнено неравенство 
.
Термины «локальный минимум» и «локальный максимум» объединены общим названием «локальный экстремум».
Теорема
(Необходимое условие существования локального экстремума). Для того чтобы функция y=f(x) имела экстремум в точке 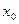, необходимо, чтобы ее производная в этой точке равнялась нулю 
или не существовала.
Геометрический смысл теоремы заключается в следующем: если в точках локальных экстремумов существуют касательные, то они параллельны оси Ox.
Точки, в которых выполнено необходимое условие экстремума называют критическими или стационарными (а также точками возможного экстремума). Очевидно, что эти точки должны входить в ОДЗ функции. Таким образом, если в какой–либо точке имеется экстремум, то эта точка критическая, однако обратное утверждение неверно: критическая точка вовсе не обязана быть точкой экстремума.
Это можно показать на примерах функций 
. Для первой функции точка 
является точкой экстремума, а для второй – нет.
Сформулируем достаточные условия существования локального экстремума.
Теорема (Первое достаточное условие экстремума)
Пусть функция f(x) дифференцируема в некоторой окрестности точки 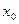. Если при переходе через точку 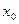слева направо производная 
меняет знак с плюса на минус, то в точке 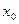функция имеет локальный максимум, а если с минуса на плюс, то 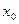– точка минимума. Если же не меняет знака в 
окрестности точки 
, то данная функция не имеет локального экстремума в этой точке.
Геометрический смысл теоремы иллюстрирует Рис. 5.9.1.
Отметим также, что дифференцируемость в самой точке 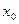вовсе не обязательна. Например, функция y=|x| имеет экстремум (минимум) в точке x= 0, но не дифференцируема в ней.
Рис. 5.9.1
Схема исследования функции y=f(x) на локальный экстремум
1. Найти производную y’=f’(x).
2. Найти критические точки функции, в которых производная f’(x)= 0 или не существует.
3. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.
4. Найти экстремумы функции.
Пример
Исследовать на экстремум функцию 
.
Решение
Найдем производную и приравняем нулю: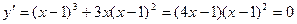 
.
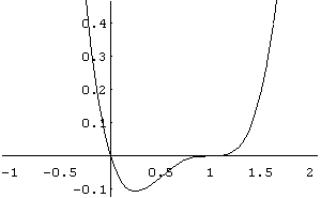
Нули производной: 
. Исследуем знаки первой производной.
Так как при переходе через точку 
производная меняет знак с минуса на плюс, то точка является точкой минимума. При переходе через точку x= 1 производная знак не меняет, поэтому точка x= 1 не является точкой экстремума.
Теорема (Второе достаточное условие экстремума)
Если первая производная f’(x) дважды дифференцируемой функции равна нулю в некоторой точке 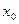, а вторая производная в этой точке положительна f’’(x)> 0, то точка есть точка минимума функции f(x); если вторая производная отрицательна – f’’(x)< 0, то – точка максимума.
Второе достаточное условие экстремума утверждает, что если в критической точке 
, то в этой точке имеется экстремум. Обратное утверждение неверно – экстремум в критической точке может быть и при равенстве нулю в ней второй производной, например, для функции 
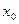и критической точки =0.
При решении прикладных задач, в частности оптимизационных, важное значение имеют задачи на нахождение наибольшего и наименьшего значений (глобального максимума и глобального минимума) функции на промежутке X.
Ранее отмечалось, что если функция y=f(x) непрерывна на отрезке [ a,b ], то она принимает на нем наибольшее и наименьшее значения. Наибольшее или наименьшее значения функции могут достигаться как в точках экстремума, так и на концах отрезка.
Для отыскания наибольшего и наименьшего значений на отрезке рекомендуется пользоваться следующей схемой:
1. Найти производную f’(x).
2. Найти критические точки функции, в которых f’(x)=0 или не существует.
3. Найти значения функции в критических точках и на концах отрезка и выбрать из них наибольшее и наименьшее.
