Как и в случае одной переменной, функция z = f (x,y) имеет узловые, определяющие структуру графика точки. В первую очередь это точки экстремума.
Определение
Точка M (x0, y0) называется точкой локального максимума (минимума) функции z = f (x,y) если существует окрестность точки M, такая, что для всех точек (x,y) из этой окрестности выполняется неравенство
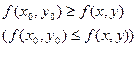
Необходимо обратить внимание на локальный характер экстремума функции, так как речь идет о максимальном и минимальном значении лишь в достаточно малой окрестности точки (x0 , y0).
Сформулируем необходимое условие экстремума – многомерный аналог теоремы Ферма.
Теорема (Необходимое условие экстремума)
Пусть точка (x0 , y0) – есть точка экстремума дифференцируемой функции z = f (x,y). Тогда частные производные 
и 
в этой точке равны нулю.
Равенство нулю частных производных в точке экстремума является необходимым, но не достаточным условием. Это видно на примере функции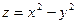 
и точки O (0,0)(Рис. 6.6.1).
Рис. 6.6.1
Частные производные функции в этой точке равны нулю, однако функция, которая является гиперболическим параболоидом, в нуле не имеет экстремума: f (0,0)=0. В любой окрестности точки O есть как положительные значения функции, так и отрицательные. Такие точки называются седловыми и являются двумерным аналогом точек перегиба функций одной переменной.
Точки, в которых выполнены необходимые условия экстремума называют критическими или стационарными.
Если частные производные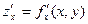 
и 
сами являются дифференцируемыми функциями, то можно найти также и их частные производные, которые называют частными производными второго порядка: 
, 
, 
, 
. Можно доказать, что если частные производные функции z = f (x,y) непрерывны в точке (x0,y0), то в этой точке 
.
Теорема (Достаточное условие экстремума функции двух переменных)
Пусть функция z = f (x,y):
а) определена в некоторой окрестности точки (x0,y0), в которой 
и 
.
б) Имеет в этой точке непрерывные частные производные второго порядка
.
Тогда если 
, то в точке (x0,y0) функция z = f (x,y) имеет экстремум, причем если A <0– минимум, A <0 если – максимум. В случае 
, функция z = f (x,y) экстремума не имеет. Если 
, то вопрос о наличии экстремума остается открытым.
Исследование функции двух переменных на экстремум
1. Найти частные производные функции 
и 
.
2. Решить систему уравнени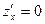й 
и 
и найти критические точки функции.
3. Найти частные производные второго порядка, вычислить их значения в каждой критической точке и с помощью достаточного условия сделать вывод о наличии экстремумов.
4. Найти экстремумы (экстремальные значения) функции.
Пример
Найти экстремумы функции 
.
Решение
1. Найдем частные производные 
, 
.
2. Найдем критические точки функции из системы уравнений 
. Система имеет решения: (1; 1), (1; –1), (–1; 1) и (–1; –1).
3. Найдем частные производные второго порядка: 
.
4. Вычислим их значения в каждой критической точке и проверяем в ней выполнение достаточного условия экстремума. Например, в точке (1; 1): А = С =–2, В =0. Так как 
и 
, то в точке (1; 1) есть точка максимума. Аналогично устанавливаем, что точка (–1; –1) – точка минимума, а точки (1; –1) и (–1; 1), в которых 
– экстремума нет. Эти точки являются седловыми.
