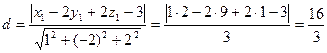Уравнение плоскости, проходящей через три точки
Если точки M0(x0;y0;z0), M1(x1;y1;z1), M2(x2;y2;z2) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:
| (2.17.1) |
Пример
Написать уравнение плоскости, проходящей через три точки: M0 (1;2;3), M1 (2;1;2), M2 (3;3;1).
Решение
Данные точки не лежат на одной прямой, так как векторы 
{1,–1,–1} и 
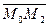{2,1,–2} не коллинеарны. Плоскость M0M1M2 представляется уравнением 
, т.е. x + z – 4 = 0.
Уравнение плоскости в отрезках
Уравнение вида
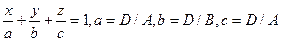
| (2.17.2) |
называется уравнением плоскости в отрезках, a, b и c –соответственно абсцисса, ордината и аппликата пересечения плоскости с осями Ox, Oy и Oz (рис. 2.17.1).
Рис. 2.17.1
Пример
Написать уравнение плоскости 3 x – 6 y +2 z – 12 = 0 в отрезках.
Решение
Очевидно, что a =4, b =–2, c =6. Тогда уравнение плоскости в отрезках есть
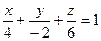
Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей
Один из углов f между плоскостями A1x + B1y + C1z + D1 = 0 и
A2x + B2y + C2z + D2 = 0 (рис. 2.18.1) равен углу между их нормальными векторами 
и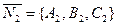 
и определяется по формуле:
| (2.18.1) |
Рис. 2.18.1
Пример
Найти угол между плоскостями x – y + 21/2 z + 2 = 0 и x + y + 21/2 z – 3 = 0.
Решение
Условие параллельности плоскостей
Две плоскости параллельны тогда и только тогда, когда их нормальные векторы 
и 
коллинеарны, следовательно, их координаты пропорциональны, т.е.
| (2.18.2) |
Пример
Определить, параллельны ли плоскости 2 x –3 y –4 z +11=0 и –4 x +6 y +8 z +36=0.
Решение
Плоскости параллельны, так как
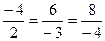
Условие перпендикулярности плоскостей
Если две плоскости заданы уравнениями A1x1 + B1y1 + C1z1 + D = 0, A2x2 + B2y2 + C2z2 + + D = 0, то условием их перпендикулярности является:
| (2.18.3) |
Если плоскости перпендикулярны, то перпендикулярны и их нормальные векторы N 1{A1,B1,C1} и N 2{A2,B2,C2}.
Пример
Определить перпендикулярны ли плоскости 3 x –2 y –2 z +7=0 и 2 x +2 y + z +4=0.
Решение
Так как 3×2+(–2)×2+(–2) ×1=0, то заданные плоскости перпендикулярны.
Плоскость, проходящая через данную точку параллельно данной плоскости
Плоскость, проходящая через точку M1(x1;y1;z1) и параллельная плоскости Ax + By + Cz + D =0, представляется уравнением:
| (3.2.7) |
Пример
Написать уравнение плоскости, проходящей через точку (2;–1;6) параллельно плоскости x + y– 2 z +5=0.
Решение:
(x –2) + (y +1) –2(z –6) = 0, т.е. x + y – 2 z + 11 = 0.
Плоскость, проходящая через две точки перпендикулярно к данной плоскости
Плоскость P, проходящая через две точки M0(x0,y0,z0) и M1(x1,y1,z1) перпендикулярно к плоскости Q, заданной уравнением Ax + By + Cz + D =0, представляется уравнением
| (2.18.4) |
Пример
Написать уравнение плоскости, проходящей через две точки: M0 (1;2;3) и M1 (2;1;1) перпендикулярно к плоскости 3 x +4 y + z –6=0.
Решение
Плоскость представляется уравнением:
, т.е. x – y + z –2=0.
Расстояние от точки до плоскости
Расстояние от точки M1(x1, y1, z1) до плоскости Ax + By + Cz + D =0 равно
| (2.18.5) |
Пример
Найти расстояние от точки (3;9;1) до плоскости x –2 y +2 z –3=0.
Решение
