Определение
Поверхностью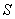 
второго порядка будем называть геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению
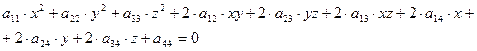
| (2.19.1) |
в котором по крайней мере один из коэффициентов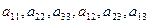 
отличен от нуля.
Уравнение (2.19.1) будем называть общим уравнением поверхности второго порядка.
Это уравнение в зависимости от значений коэффициентов aij может определять сферу, эллипсоид, однополосный или двуполостный гиперболоид, эллиптический или гиперболический параболоид, цилиндрическую или коническую поверхность второго порядка.
В декартовых прямоугольных координатах сфера, имеющая центр в точке с координатами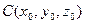 
и радиус r,определяется уравнением
 .
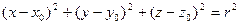| (2.19.2) |
Сфера радиуса 
, центр которой находится в начале координат, имеет уравнение
 .
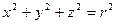| (2.19.3) |
Эллипсоид
Определение
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
 ,
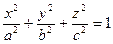| (2.20.1) |
где a, b, c – полуоси эллипсоида (рис. 2.20.1).
Уравнение (2.20.1) называется каноническим уравнением эллипсоида. Эллипсоид, у которого все полуоси различны, называется трехосным. В том случае, когда какие–нибудь две из полуосей одинаковы, эллипсоид является поверхностью вращения, т.е. такой эллипсоид получен вращением эллипса вокруг одной из осей. Центр симметрии эллипсоида (2.20.1) совпадает с началом координат.
Если центр эллипсоида перенесен в точку 
, то его каноническое уравнение принимает вид
 .
| (2.20.2) |
Рис. 2.20.1
Гиперболоиды
Определение
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются каноническими уравнениями вида
 ,
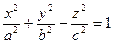| (2.21.1) |
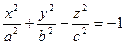
| (2.21.2) |
| 
|
| Рис. 2.21.1 | Рис. 2.21.2 |
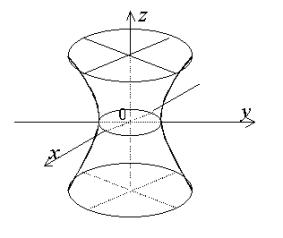
Гиперболоид, определяемый уравнением (2.21.1) называется однополостным (Рис. 2.21.1); гиперболоид, определяемый уравнением (2.21.2), – двуполостным (Рис. 2.21.2). Величины a, b, c называются полуосями гиперболоида. Центр симметрии в уравнениях (2.26.1) и (2.26.2) совпадает с началом координат.
Ось Oz является осью однополостного гиперболоида. Горизонтальные плоскости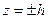 
пересекают однополостный гиперболоид (Рис. 2.21.1) по эллипсам, причем наименьший (“горловой”) эллипс получается при 
и определяется уравнением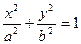 
. Вертикальные плоскости пересекают однополостный гиперболоид по гиперболам (Рис. 2.21.1). Гиперболоид, у которого полуоси a и b равны, является поверхностью вращения гиперболы вокруг оси Oz.
Если центр перенести в точку , то каноническое уравнение однополостного гиперболоида принимает вид
 .
| (2.21.3) |
Поверхность двуполостного гиперболоида имеет две вершины в точках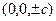 
расположенных на оси Oz (Рис. 2.21.2). Горизонтальные плоскости 
пересекают поверхность двуполостного гиперболоида по эллипсам, вертикальные – по гиперболам. Гиперболоид, у которого полуоси a и b равны, является поверхностью вращения гиперболы вокруг оси Oz.
Каноническое уравнение двуполостного гиперболоида со смещенным центром имеет вид
 .
| (2.21.4) |
Параболоиды
Определение
Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями
 ,
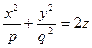| (2.22.1) |
 ,
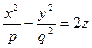| (2.22.2) |
где p и q – положительные числа, называемые параметрами параболы.
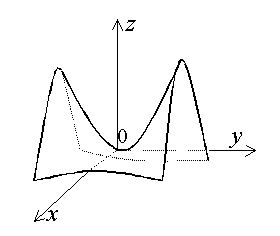
Параболоид, определяемый уравнением (2.22.1), называется эллиптическим (Рис. 2.22.1); параболоид, определяемый уравнением (2.22.2), называется гиперболическим (Рис. 2.22.2). Уравнения (2.22.1) и (2.22.2) называют каноническими уравнениями соответствующих параболоидов.
Осью эллиптического параболоида является к оординатная ось Oz. Его вершина находится в начале координат. Горизонтальные плоскости z=h, h>0 пересекают поверхность эллиптического параболоида по эллипсам, вертикальные – по параболам. В случае, когда p=q, параболоид, определяемый уравнением (2.22.1), является поверхностью вращения (вокруг оси Oz). Каноническое уравнение эллиптического параболоида со смещенным центром имеет вид
 .
| (2.22.3) |
| 
|
| Рис. 2.22.1 | Рис. 2.22.2 |
Ось гиперболического параболоида совпадает с осью I Oz. Горизонтальные плоскости z=h пересекают поверхность параболоида по гиперболам, причем гиперболы, полученные при h>0, сопряжены с гиперболами, полученными при h<0. Вертикальные плоскости пересекают поверхность параболоида по параболам.
