Определение
Постоянной величиной называется величина, сохраняющая одно и тоже значение.
Например, отношение длины окружности к ее диаметру есть постоянная величина, равная p.
Определение
Если величина сохраняет постоянное значение лишь в условиях данного процесса, то в этом случае она называется параметром.
Определение
Переменной называется величина, которая может принимать различные числовые значения.
Например, при равномерном движении S = vt, где путь S и время t – переменные величины, а v – параметр.
Определение
Если каждому элементу x множества X 
ставится в соответствие вполне определенный элемент y множества Y 
, то говорят, что на множестве X задана функция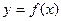 
.
При этом x называется независимой переменной (или аргументом), y –зависимой переменной, а буква f обозначает закон соответствия.
Множество X называется областью определения (или существования) функции, а множество Y – областью значений функции. Если множество X специально не оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменной x, т.е. множество таких значений x, при которых функция y = f (x) вообще имеет смысл.
Например, область определения функции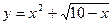 
есть полуинтервал 
, так как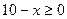 
; если же переменная x обозначает, предположим, время, то при естественном дополнительном условии 
областью определения функции будет отрезок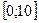 
.
Способы задания функций
Задать функцию – значит указать закон, по которому, согласно определению, каждому значению аргумента из области определения ставится в соответствие значение функции из области значений функций. Существует три основных способа задания функций: табличный, аналитический и графический.
Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента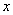 
и соответствующие значения функции 
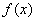, например таблица логарифмов. Табличный способ имеет широкое применение в различных отраслях знаний и приложениях: ряды экспериментальных измерений, социологические опросы, таблицы бухгалтерской отчетности и банковской деятельности и т.п.
Аналитический способ состоит в задании связи 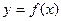между аргументом и функцией в виде формул.Этот способ наиболее часто встречается на практике. Так, функция 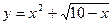,рассматриваемая выше, задана аналитически. Не следует смешивать функцию с ее аналитическим выражением. Так, например, одна функция
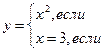
имеет два аналитических выражения, используемых при различных значениях аргумента.
Графический способ состоит в том, что соответствие между аргументом и функцией задается посредством графика. Этот способ обычно используется в экспериментальных измерениях и употреблением самопишущих приборов (осциллографы, сейсмографы и т.д.).
Основные свойства функции
1. Четность и нечетность.
Функция 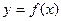называется четной, если для любых значений 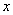из области определения 
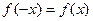и нечетной, если 
. В противном случае функция 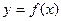называется функцией общего вида.
Например, функция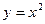 
является четной, а функция 
– нечетной. Функция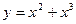 
является функцией общего вида, так как 
и 
и 
.
Графикчетной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
2. Монотонность.
Функция 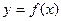называется возрастающей (убывающей) на промежутке 
, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
Пусть 
и 
. Тогда функция возрастает на промежутке X, если 
и убывает, если 
.
Функции возрастающие и убывающие называются монотонными функциями.
Так, например, функция 
при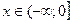 
убывает и при 
– возрастает.
3. Ограниченность.
Функция 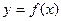называется ограниченной на промежутке X, если существует такое положительное число M>0, что 
для любого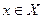 
.
Например, функция 
ограничена на всей числовой оси, так как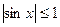 
для любого 
.
4. Периодичность.
Функция 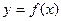называется периодической с периодом 
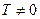, если для любых x из области определения функции 
.
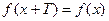Например, функция имеет период 
, так как для любых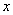 
.
